Công Thức đường Trung Tuyến Lớp 10 là một trong những công thức quan trọng trong hình học phẳng, giúp học sinh giải quyết nhiều bài toán liên quan đến tam giác. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về công thức này, từ định nghĩa, cách chứng minh, đến các dạng bài tập thường gặp và mẹo ghi nhớ hiệu quả. tổng hợp các công thức vật lý thcs
Định Nghĩa Đường Trung Tuyến và Công Thức Liên Quan
Đường trung tuyến của một tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Công thức đường trung tuyến lớp 10 được biểu diễn như sau: ma² = (2b² + 2c² – a²) / 4. Trong đó, ma là độ dài đường trung tuyến kẻ từ đỉnh A, a, b, c lần lượt là độ dài các cạnh BC, AC, AB. Tương tự, ta có công thức cho các đường trung tuyến kẻ từ đỉnh B và C.
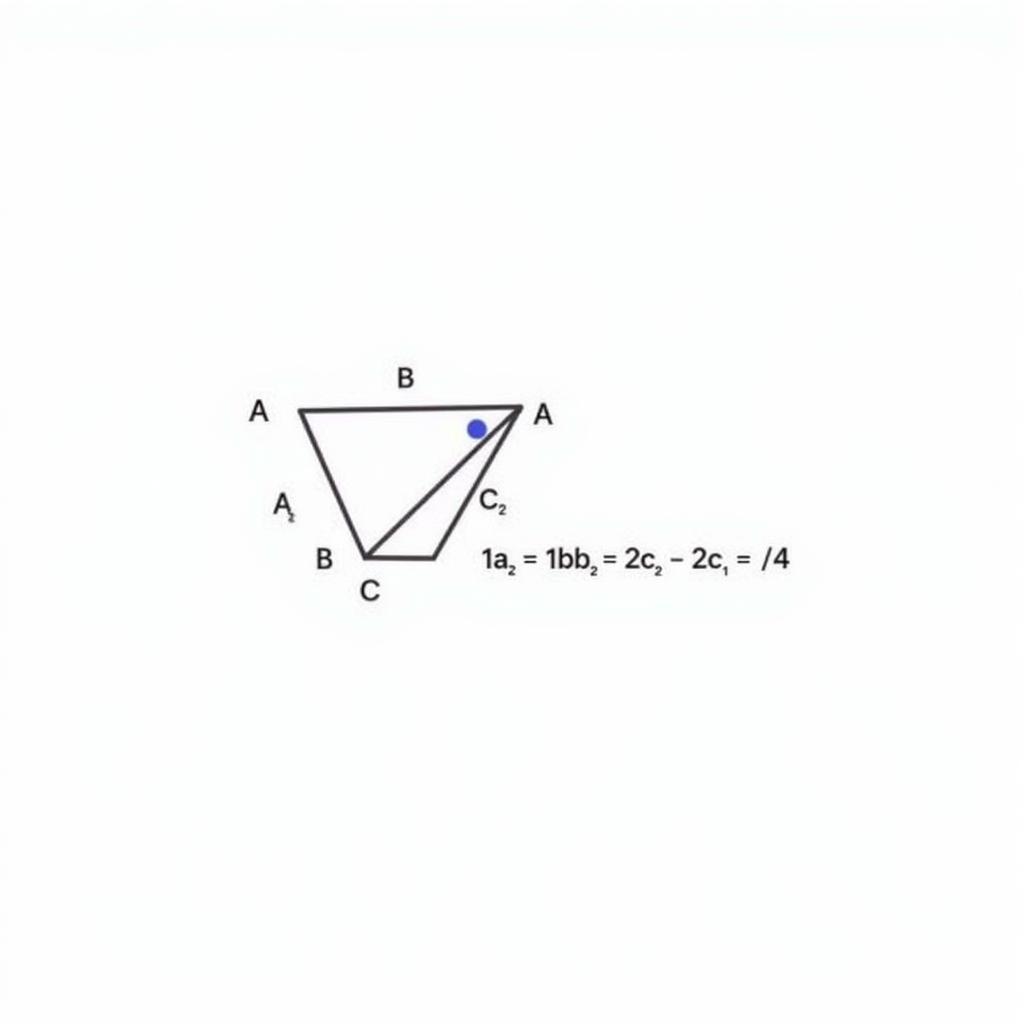 Công thức đường trung tuyến
Công thức đường trung tuyến
Chứng Minh Công Thức Đường Trung Tuyến
Có nhiều cách chứng minh công thức đường trung tuyến. Một trong những cách phổ biến nhất là sử dụng định lý cosin. Xét tam giác ABC, gọi M là trung điểm của BC. Áp dụng định lý cosin cho tam giác ABM và ACM, ta sẽ thu được công thức đường trung tuyến.
Ứng Dụng Công Thức Đường Trung Tuyến trong Giải Toán
Công thức đường trung tuyến có ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến độ dài đoạn thẳng, tính diện tích tam giác, chứng minh các hệ thức hình học…
Tính Độ Dài Đường Trung Tuyến
Khi biết độ dài ba cạnh của tam giác, ta có thể dễ dàng tính được độ dài của bất kỳ đường trung tuyến nào bằng cách áp dụng công thức.
Tính Độ Dài Cạnh Tam Giác
Ngược lại, nếu biết độ dài hai cạnh và một đường trung tuyến, ta cũng có thể tính được độ dài cạnh còn lại của tam giác. công thức tính cạnh tam giác thường
Chứng Minh Hệ Thức Hình Học
Công thức đường trung tuyến cũng được sử dụng để chứng minh các hệ thức hình học khác trong tam giác.
Trả Lời Các Câu Hỏi
What công thức đường trung tuyến lớp 10?
Công thức đường trung tuyến lớp 10 là ma² = (2b² + 2c² – a²) / 4, với ma là đường trung tuyến kẻ từ đỉnh A, a, b, c là độ dài các cạnh BC, AC, AB.
Who sử dụng công thức đường trung tuyến lớp 10?
Học sinh lớp 10 và những ai nghiên cứu về hình học.
When học công thức đường trung tuyến lớp 10?
Công thức này thường được học trong chương trình Toán lớp 10.
Where áp dụng công thức đường trung tuyến lớp 10?
Công thức này được áp dụng trong các bài toán hình học liên quan đến tam giác.
Why cần học công thức đường trung tuyến lớp 10?
Công thức này là nền tảng quan trọng để giải quyết nhiều bài toán hình học phẳng.
How ghi nhớ công thức đường trung tuyến lớp 10?
Có thể ghi nhớ bằng cách liên tưởng đến định lý cosin hoặc thông qua việc luyện tập thường xuyên.
“Việc nắm vững công thức đường trung tuyến không chỉ giúp học sinh giải toán hiệu quả mà còn rèn luyện tư duy logic và khả năng phân tích vấn đề,” – Nguyễn Văn A, Giáo viên Toán THPT chuyên Nguyễn Huệ.
Mẹo Ghi Nhớ Công Thức Đường Trung Tuyến
Để ghi nhớ công thức này một cách dễ dàng, bạn có thể sử dụng các mẹo sau: Viết công thức ra giấy nhiều lần. Liên hệ công thức với định lý cosin. Làm nhiều bài tập áp dụng công thức.
“Luyện tập thường xuyên là chìa khóa để thành thạo bất kỳ công thức toán học nào, bao gồm cả công thức đường trung tuyến,” – Trần Thị B, Giảng viên Đại học Sư phạm Hà Nội.
Kết luận
Công thức đường trung tuyến lớp 10 là một công cụ quan trọng trong việc giải quyết các bài toán hình học. Hiểu rõ công thức này và luyện tập thường xuyên sẽ giúp bạn nâng cao khả năng giải toán và đạt điểm cao trong các kỳ thi. công thức tính diện tích tam giác lớp 9
FAQ
1. Công thức đường trung tuyến áp dụng cho tam giác nào?
Áp dụng cho mọi loại tam giác.
2. Có bao nhiêu đường trung tuyến trong một tam giác?
Một tam giác có ba đường trung tuyến.
3. Điểm đồng quy của ba đường trung tuyến gọi là gì?
Gọi là trọng tâm của tam giác.
4. Công thức đường trung tuyến có liên quan gì đến định lý Stewart?
Định lý Stewart là một dạng tổng quát hơn của công thức đường trung tuyến.
5. Làm thế nào để phân biệt đường trung tuyến và đường cao trong tam giác?
Đường trung tuyến nối đỉnh với trung điểm cạnh đối diện, đường cao vuông góc với cạnh đối diện.
6. Ngoài công thức đường trung tuyến, còn công thức nào liên quan đến trung tuyến nữa không?
Có, ví dụ như công thức tính độ dài đường trung tuyến theo tọa độ đỉnh.
7. công thức tính vận tốc lớp 8 Có tài liệu nào hướng dẫn chi tiết về công thức đường trung tuyến không?
Có rất nhiều sách giáo khoa và tài liệu trực tuyến về chủ đề này.
8. Công thức đường trung tuyến có ứng dụng trong thực tế không?
Có, nó được ứng dụng trong các lĩnh vực như xây dựng, kiến trúc, đồ họa máy tính…
9. Làm thế nào để giải bài toán tìm đường trung tuyến khi biết tọa độ các đỉnh?
Sử dụng công thức tính độ dài đoạn thẳng trong hệ tọa độ.
10. Có phần mềm nào hỗ trợ tính toán đường trung tuyến không?
GeoGebra là một ví dụ.
