Công thức tính vecto pháp tuyến trong không gian là một kiến thức quan trọng trong hình học không gian, giúp chúng ta giải quyết nhiều bài toán liên quan đến mặt phẳng. Vecto pháp tuyến đóng vai trò then chốt trong việc xác định phương trình mặt phẳng và tính toán các đại lượng hình học khác.
Vecto Pháp Tuyến Là Gì?
Vecto pháp tuyến của một mặt phẳng là một vecto không-null vuông góc với mọi vecto nằm trên mặt phẳng đó. Nói cách khác, nếu ta có một mặt phẳng (P) và một vecto $vec{n}$ sao cho $vec{n}$ vuông góc với mọi vecto nằm trên (P), thì $vec{n}$ được gọi là vecto pháp tuyến của mặt phẳng (P). Việc hiểu rõ định nghĩa này là bước đầu tiên để nắm vững công thức tính vecto pháp tuyến.
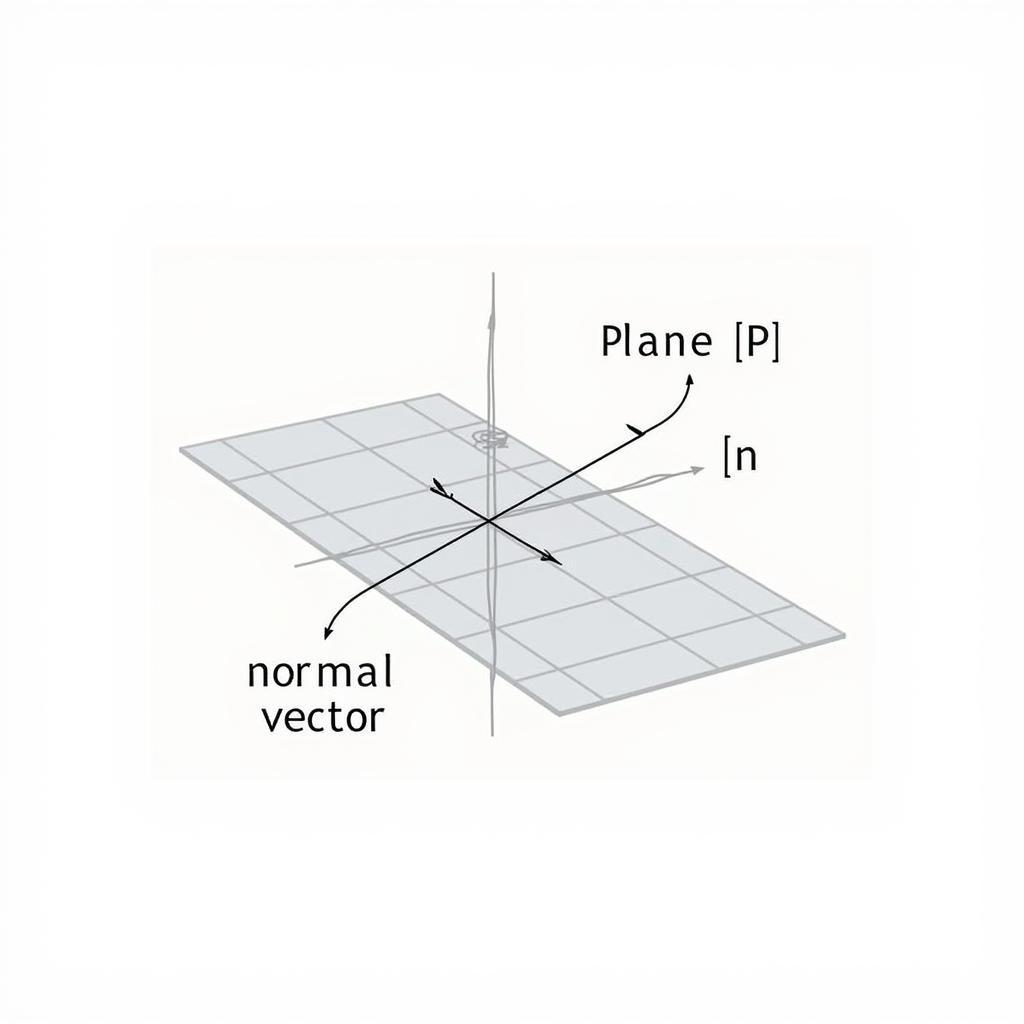Vecto Pháp Tuyến Mặt Phẳng
Các Công Thức Tính Vecto Pháp Tuyến Trong Không Gian
Có nhiều cách để xác định vecto pháp tuyến của một mặt phẳng, tùy thuộc vào thông tin đã cho. Dưới đây là một số công thức phổ biến:
-
Từ Phương Trình Tổng Quát Của Mặt Phẳng: Nếu phương trình tổng quát của mặt phẳng (P) là Ax + By + Cz + D = 0, thì vecto pháp tuyến của (P) là $vec{n}$(A, B, C). Đây là cách đơn giản nhất để tìm vecto pháp tuyến. Bạn có thể tìm hiểu thêm về công thức phương trình tổng quát.
-
Từ Ba Điểm Không Thẳng Hàng: Nếu biết ba điểm A(x₁, y₁, z₁), B(x₂, y₂, z₂), C(x₃, y₃, z₃) không thẳng hàng thuộc mặt phẳng (P), ta có thể tính vecto pháp tuyến bằng cách tính tích có hướng của hai vecto $vec{AB}$ và $vec{AC}$: $vec{n} = vec{AB} times vec{AC}$.
-
Từ Hai Vecto Không Song Song: Tương tự như trên, nếu biết hai vecto $vec{u}$ và $vec{v}$ không song song và cùng nằm trên mặt phẳng (P), ta có thể tính vecto pháp tuyến bằng tích có hướng: $vec{n} = vec{u} times vec{v}$. Kiến thức về công thức hình học lớp 12 học kì 1 sẽ giúp bạn nắm vững hơn phần này.
Trả Lời Các Câu Hỏi:
-
What công thức tính vecto pháp tuyến trong không gian? Công thức tính vecto pháp tuyến phụ thuộc vào thông tin đã cho, có thể từ phương trình mặt phẳng, ba điểm hoặc hai vecto trên mặt phẳng.
-
Who sử dụng công thức tính vecto pháp tuyến trong không gian? Học sinh, sinh viên, và những người làm việc trong lĩnh vực liên quan đến toán học và hình học không gian.
-
When cần sử dụng công thức tính vecto pháp tuyến trong không gian? Khi cần xác định phương trình mặt phẳng, tính góc giữa hai mặt phẳng, khoảng cách từ điểm đến mặt phẳng, v.v.
-
Where áp dụng công thức tính vecto pháp tuyến trong không gian? Trong hình học không gian, vật lý, đồ họa máy tính, và nhiều lĩnh vực khác.
-
Why công thức tính vecto pháp tuyến trong không gian quan trọng? Vì vecto pháp tuyến là yếu tố quan trọng để xác định và nghiên cứu các tính chất của mặt phẳng.
-
How tính vecto pháp tuyến trong không gian? Sử dụng một trong các công thức đã nêu, tùy thuộc vào thông tin bài toán cung cấp. Việc nắm vững công thức hình chiếu cũng sẽ hỗ trợ rất nhiều.
Ví Dụ Minh Họa
Cho mặt phẳng (P) đi qua ba điểm A(1,0,0), B(0,2,0) và C(0,0,3). Tính vecto pháp tuyến của (P).
Ta có $vec{AB}$(-1,2,0) và $vec{AC}$(-1,0,3). Vậy $vec{n} = vec{AB} times vec{AC}$ = (6,3,2). Đây là một ví dụ cụ thể về cách áp dụng công thức tính vecto pháp tuyến từ ba điểm. Việc hiểu chứng minh công thức tính đường trung tuyến cũng giúp bạn có cái nhìn sâu sắc hơn về hình học không gian.
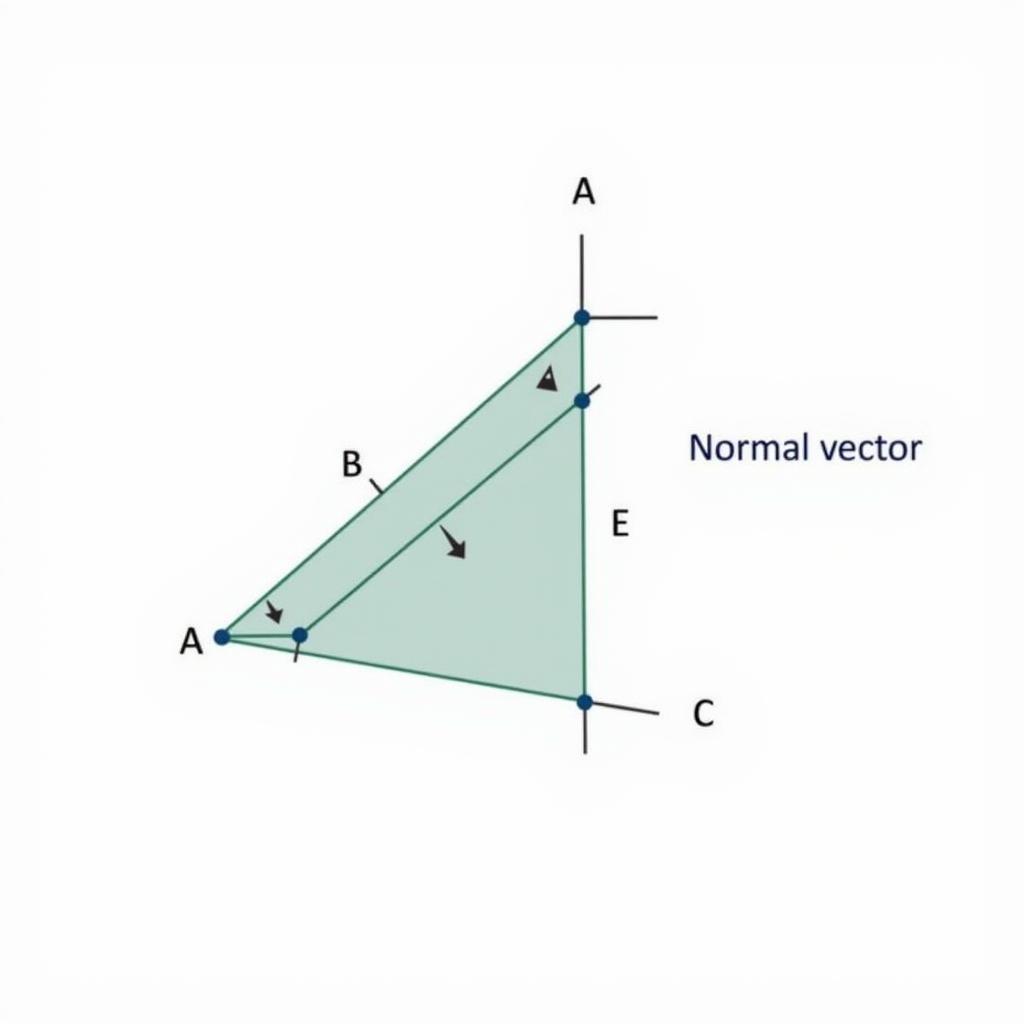Ví Dụ Vecto Pháp Tuyến
Kết luận
Công thức tính vecto pháp tuyến trong không gian là một công cụ quan trọng trong hình học. Hiểu rõ các công thức và cách áp dụng chúng sẽ giúp bạn giải quyết nhiều bài toán liên quan đến mặt phẳng một cách hiệu quả.
FAQ
-
Nêu Câu Hỏi: Vecto pháp tuyến có duy nhất không?
Trả Lời Chi tiết Câu Hỏi: Một mặt phẳng có vô số vecto pháp tuyến, chúng đều cùng phương với nhau. -
Nêu Câu Hỏi: Làm thế nào để kiểm tra xem một vecto có phải là vecto pháp tuyến của mặt phẳng hay không?
Trả Lời Chi tiết Câu Hỏi: Kiểm tra xem vecto đó có vuông góc với hai vecto không song song bất kỳ nằm trên mặt phẳng hay không. -
Nêu Câu Hỏi: Ứng dụng của vecto pháp tuyến trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Vecto pháp tuyến được sử dụng trong đồ họa máy tính, vật lý, và nhiều lĩnh vực kỹ thuật khác. -
Nêu Câu Hỏi: Tích có hướng của hai vecto là gì?
Trả Lời Chi tiết Câu Hỏi: Tích có hướng của hai vecto là một vecto vuông góc với cả hai vecto ban đầu. -
Nêu Câu Hỏi: Làm thế nào để tính góc giữa hai mặt phẳng?
Trả Lời Chi tiết Câu Hỏi: Góc giữa hai mặt phẳng được tính bằng góc giữa hai vecto pháp tuyến của chúng. Bạn có thể tìm hiểu thêm về công thức tính diện tích tam giác oab.