Công Thức Tính Dây Cung Của đường Tròn là một kiến thức toán học quan trọng, giúp chúng ta giải quyết nhiều bài toán hình học phức tạp. Bài viết này sẽ cung cấp cho bạn cái nhìn chi tiết về công thức này, cùng với các ví dụ minh họa và câu hỏi thường gặp.
Khám Phá Công Thức Tính Dây Cung
Dây cung là một đoạn thẳng nối hai điểm bất kỳ trên đường tròn. Để tính độ dài dây cung, chúng ta có thể sử dụng nhiều công thức khác nhau, tùy thuộc vào dữ kiện bài toán cho trước. Công thức phổ biến nhất là sử dụng sin của góc chắn cung và bán kính đường tròn.
Công Thức Sử Dụng Bán Kính và Góc Ở Tâm
Nếu biết bán kính (R) và góc ở tâm (α) chắn cung, độ dài dây cung (l) được tính theo công thức: l = 2Rsin(α/2). Công thức này khá đơn giản và dễ áp dụng.
Công Thức Sử Dụng Bán Kính và Khoảng Cách Từ Tâm Đến Dây Cung
Nếu biết bán kính (R) và khoảng cách từ tâm đường tròn đến dây cung (d), ta có thể tính độ dài dây cung (l) bằng định lý Pythagoras: l = 2√(R² - d²).
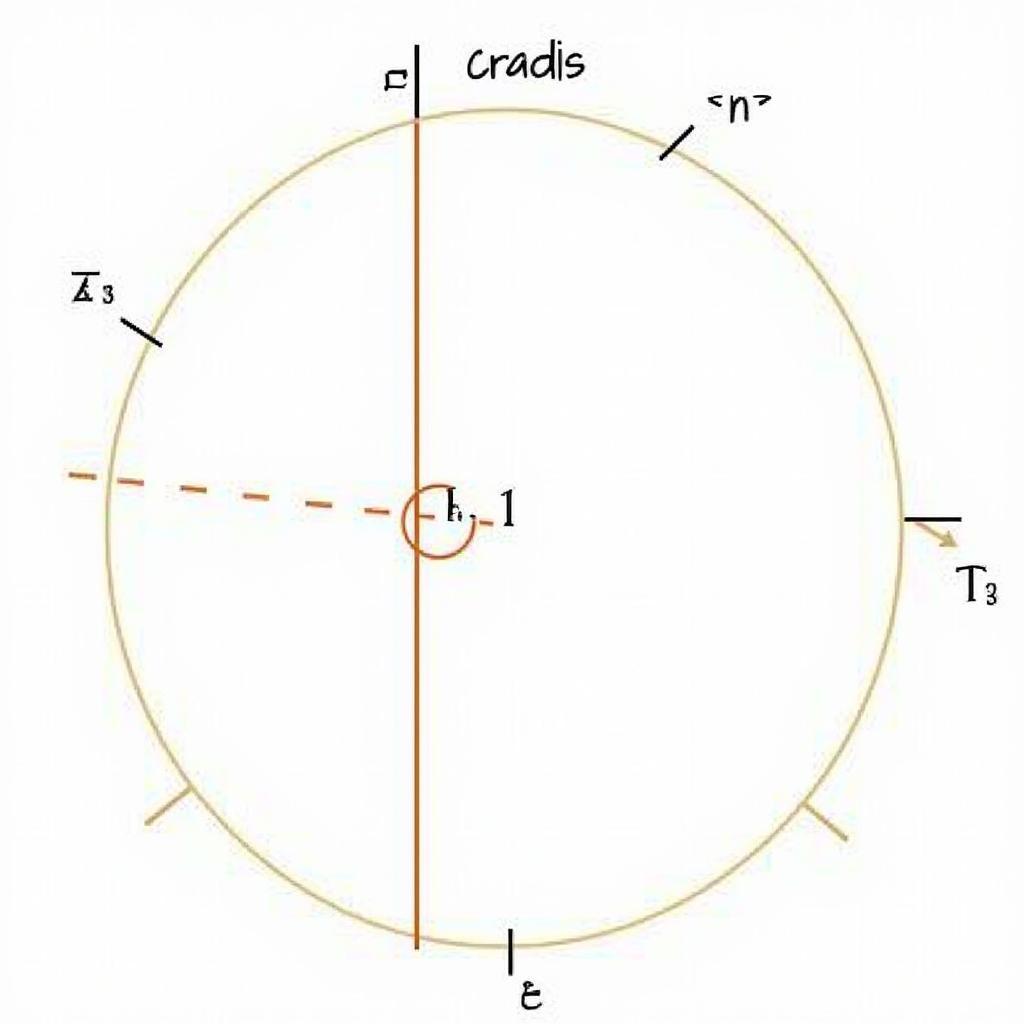Công Thức Dây Cung Bán Kính Khoảng Cách
Các Trường Hợp Đặc Biệt Của Dây Cung
Một trường hợp đặc biệt của dây cung là đường kính, đây là dây cung dài nhất của đường tròn. Đường kính có độ dài gấp đôi bán kính. công thức toán hình học không gian lớp 12 có thể giúp bạn hiểu rõ hơn về hình học không gian liên quan.
Dây Cung và Các Góc Liên Quan
Góc ở tâm chắn một cung có số đo gấp đôi góc nội tiếp chắn cùng cung đó. Kiến thức này rất hữu ích khi giải các bài toán liên quan đến dây cung và góc. công thức sin có cũng là kiến thức nền tảng giúp bạn hiểu rõ hơn về mối quan hệ giữa góc và cạnh trong tam giác.
Trả Lời Các Câu Hỏi
- What “công thức tính dây cung của đường tròn”?: Công thức tính dây cung đường tròn giúp xác định độ dài đoạn thẳng nối hai điểm trên đường tròn, dựa trên bán kính, góc ở tâm hoặc khoảng cách từ tâm đến dây cung.
- Who “công thức tính dây cung của đường tròn”?: Học sinh, sinh viên, kỹ sư, và bất kỳ ai làm việc với hình học đều sử dụng công thức này.
- When “công thức tính dây cung của đường tròn”?: Công thức này được sử dụng khi cần tính toán độ dài dây cung trong các bài toán hình học.
- Where “công thức tính dây cung của đường tròn”?: Công thức này được áp dụng trong toán học, vật lý, kỹ thuật, và nhiều lĩnh vực khác.
- Why “công thức tính dây cung của đường tròn”?: Công thức này giúp đơn giản hóa việc tính toán độ dài dây cung, thay vì phải đo trực tiếp.
- How “công thức tính dây cung của đường tròn”?: Độ dài dây cung được tính bằng
l = 2Rsin(α/2)hoặcl = 2√(R² - d²).
Kết Luận
Công thức tính dây cung của đường tròn là một công cụ quan trọng trong hình học. Hiểu rõ và áp dụng thành thạo công thức này sẽ giúp bạn giải quyết nhiều bài toán phức tạp. công thức hình chỏm cầu cũng liên quan đến đường tròn và có thể hữu ích cho bạn.
FAQ
-
Nêu Câu Hỏi: Làm thế nào để nhớ công thức tính dây cung?
Trả Lời Chi tiết Câu Hỏi: Bạn có thể liên tưởng đến hình tam giác vuông được tạo bởi bán kính, khoảng cách từ tâm đến dây và một nửa dây cung để nhớ công thứcl = 2√(R² - d²). Còn công thứcl = 2Rsin(α/2)có thể ghi nhớ bằng cách luyện tập thường xuyên. -
Nêu Câu Hỏi: Công thức tính dây cung có ứng dụng gì trong thực tế?
Trả Lời Chi tiết Câu Hỏi: Công thức này được ứng dụng trong nhiều lĩnh vực, ví dụ như xây dựng, thiết kế, thiên văn học. công thức chương 3 vật lý 10 cũng có thể liên quan đến ứng dụng của công thức này. -
Nêu Câu Hỏi: Nếu chỉ biết độ dài dây cung và bán kính, làm sao tính góc ở tâm?
Trả Lời Chi tiết Câu Hỏi: Bạn có thể biến đổi công thứcl = 2Rsin(α/2)thànhα = 2arcsin(l/2R)để tính góc ở tâm. -
Nêu Câu Hỏi: Có công thức nào khác để tính dây cung không?
Trả Lời Chi tiết Câu Hỏi: Có, ngoài hai công thức trên, còn có thể sử dụng công thức liên quan đến diện tích tam giác tạo bởi hai bán kính và dây cung. -
Nêu Câu Hỏi: Dây cung có liên quan gì đến tiếp tuyến của đường tròn?
Trả Lời Chi tiết Câu Hỏi: Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm, và nếu kẻ đường kính từ tiếp điểm thì đường kính đó sẽ vuông góc với tiếp tuyến. Dây cung đi qua tiếp điểm và vuông góc với đường kính đó.