Công Thức Delta là một công cụ quan trọng trong toán học, đặc biệt là trong việc giải quyết các phương trình bậc hai. Nó giúp chúng ta xác định số lượng và tính chất của nghiệm, mở ra cánh cửa cho việc áp dụng vào nhiều lĩnh vực khác nhau. Chúng ta sẽ cùng nhau khám phá sức mạnh của công thức delta, từ khái niệm cơ bản đến những ứng dụng thú vị.
Công Thức Delta Là Gì?
Công thức delta, thường được ký hiệu là Δ (delta), được dùng để tính toán biệt thức của phương trình bậc hai dạng ax² + bx + c = 0 (với a ≠ 0). Công thức này được định nghĩa là: Δ = b² – 4ac.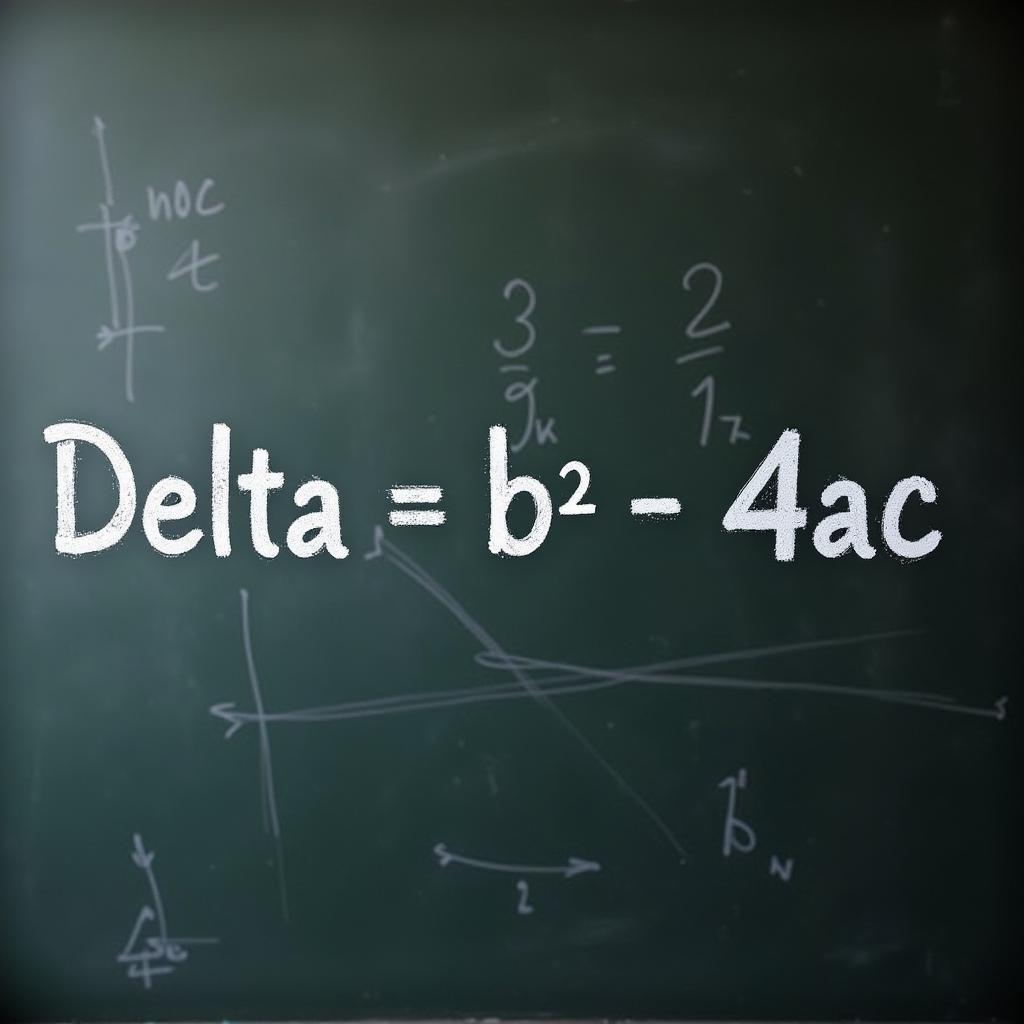 
Công thức delta
Giá trị của delta cho ta biết phương trình có bao nhiêu nghiệm và loại nghiệm đó là gì. Nếu Δ > 0, phương trình có hai nghiệm phân biệt. Nếu Δ = 0, phương trình có nghiệm kép. Và nếu Δ < 0, phương trình không có nghiệm thực. Việc nắm vững công thức delta là bước đầu tiên để giải quyết các bài toán liên quan đến phương trình bậc hai.
Ứng Dụng Của Công Thức Delta Trong Toán Học
Công thức delta không chỉ giúp ta tìm nghiệm của phương trình bậc hai mà còn có nhiều ứng dụng khác trong toán học. Ví dụ, nó giúp xác định vị trí tương đối giữa parabol và trục hoành, tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số bậc hai, và giải quyết các bài toán liên quan đến hình học. 
Ứng dụng của công thức delta
Công Thức Nghiệm Của Phương Trình Bậc Hai
Khi Δ ≥ 0, ta có thể tính nghiệm của phương trình bậc hai bằng công thức nghiệm:
- x₁ = (-b + √Δ) / 2a
- x₂ = (-b – √Δ) / 2a
viết công thức nghiệm tổng quát
What Công Thức Delta?
Công thức delta là một công thức toán học dùng để tính biệt thức của phương trình bậc hai.
Who Sử Dụng Công Thức Delta?
Học sinh, sinh viên, giáo viên, và những người làm việc trong các lĩnh vực liên quan đến toán học đều sử dụng công thức delta.
When Sử Dụng Công Thức Delta?
Công thức delta được sử dụng khi cần giải quyết các bài toán liên quan đến phương trình bậc hai.
Where Tìm Hiểu Về Công Thức Delta?
Bạn có thể tìm hiểu về công thức delta trong sách giáo khoa toán, trên internet, hoặc từ giáo viên.
Why Công Thức Delta Quan Trọng?
Công thức delta quan trọng vì nó giúp ta hiểu rõ hơn về tính chất của phương trình bậc hai và giải quyết nhiều bài toán liên quan.
How Tính Công Thức Delta?
Để tính công thức delta, ta sử dụng công thức Δ = b² – 4ac.
Ví Dụ Về Công Thức Delta
Xét phương trình x² – 4x + 3 = 0. Ta có a = 1, b = -4, và c = 3.
Δ = (-4)² – 4 1 3 = 16 – 12 = 4. Vì Δ > 0, phương trình có hai nghiệm phân biệt.
x₁ = (4 + √4) / 2 = 3
x₂ = (4 – √4) / 2 = 1
công thức tính delta phương trình bậc 3
“Công thức delta là nền tảng cho việc hiểu và giải quyết các bài toán liên quan đến phương trình bậc hai.” – GS. Nguyễn Văn A, Chuyên gia Toán học.
công thức nghiệm của phương trình bậc hai toán 9
Ví dụ công thức delta
“Việc thành thạo công thức delta giúp học sinh tự tin hơn trong việc giải quyết các bài toán phức tạp.” – ThS. Trần Thị B, Giáo viên Toán.
Kết luận
Công thức delta là một công cụ mạnh mẽ và không thể thiếu trong việc giải quyết các bài toán liên quan đến phương trình bậc hai. Hiểu rõ về công thức delta sẽ giúp bạn nắm vững kiến thức toán học và áp dụng vào nhiều lĩnh vực khác nhau.
FAQ
- Nêu Công Thức Delta? Δ = b² – 4ac.
- Delta dùng để làm gì? Xác định số nghiệm và tính chất nghiệm của phương trình bậc hai.
- Phương trình bậc hai có nghiệm khi nào? Khi Δ ≥ 0.
- Phương trình bậc hai vô nghiệm khi nào? Khi Δ < 0.
- Công thức nghiệm của phương trình bậc hai là gì? x = (-b ± √Δ) / 2a.
- Làm thế nào để tính delta cho phương trình bậc hai dạng ax² + bx + c = 0? Thay các giá trị a, b, c vào công thức Δ = b² – 4ac.
- Delta có ứng dụng gì trong đời sống? Ứng dụng trong vật lý, kỹ thuật, kinh tế,…
- Tại sao cần học công thức delta? Giúp giải quyết các bài toán liên quan đến phương trình bậc hai và hiểu sâu hơn về toán học.
- Có công thức delta cho phương trình bậc ba không? Có, nhưng phức tạp hơn.
- Tài liệu nào giúp tôi học thêm về công thức delta? Sách giáo khoa toán, website giáo dục, video bài giảng trực tuyến.