Công Thức Tính Cạnh Huyền Hình Tam Giác Vuông là một kiến thức cơ bản nhưng vô cùng quan trọng trong toán học, đặc biệt là hình học. Nắm vững công thức này sẽ giúp bạn giải quyết nhiều bài toán liên quan đến tam giác vuông một cách dễ dàng. Bài viết này sẽ cung cấp cho bạn mọi thứ bạn cần biết về công thức tính cạnh huyền, từ định nghĩa, công thức, đến các ví dụ minh họa và ứng dụng thực tiễn.
Định Nghĩa Cạnh Huyền và Định Lý Pythagore
Cạnh huyền là cạnh đối diện với góc vuông trong một tam giác vuông. Định lý Pythagore, một trong những định lý nổi tiếng nhất trong toán học, chính là chìa khóa để tính độ dài cạnh huyền. Định lý này phát biểu rằng: “Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông”.
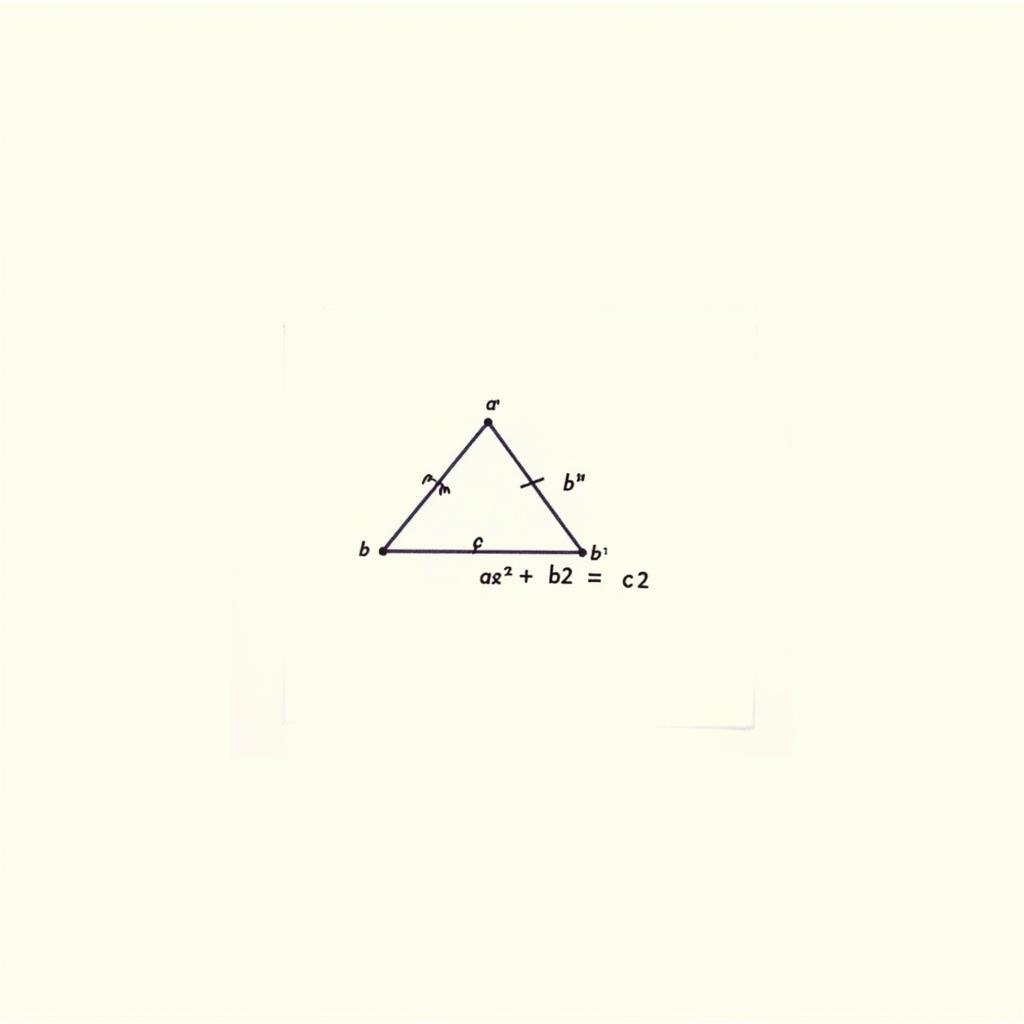 Minh họa Định Lý Pythagore trên Tam Giác Vuông
Minh họa Định Lý Pythagore trên Tam Giác Vuông
Công Thức Tính Cạnh Huyền Hình Tam Giác Vuông
Dựa trên định lý Pythagore, công thức tính cạnh huyền (c) của một tam giác vuông có hai cạnh góc vuông lần lượt là a và b được biểu diễn như sau:
c = √(a² + b²)Trong đó:
c: Độ dài cạnh huyềna,b: Độ dài hai cạnh góc vuông
Công thức này cho phép chúng ta tính toán độ dài cạnh huyền khi biết độ dài hai cạnh góc vuông. Bạn có muốn tìm hiểu thêm về các công thức liên quan đến diện tích và thể tích của các hình khác? Hãy xem bài viết công thức diện tích thể tích các hình.
Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng công thức, hãy cùng xem một vài ví dụ:
- Ví dụ 1: Một tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Tính độ dài cạnh huyền.
c = √(3² + 4²) = √(9 + 16) = √25 = 5cm- Ví dụ 2: Một tam giác vuông có một cạnh góc vuông là 5cm và cạnh huyền là 13cm. Tính độ dài cạnh góc vuông còn lại.
Trong trường hợp này, ta cần biến đổi công thức:
b = √(c² - a²) = √(13² - 5²) = √(169 - 25) = √144 = 12cmỨng Dụng Thực Tiễn
Công thức tính cạnh huyền có rất nhiều ứng dụng trong thực tế, từ xây dựng, kiến trúc đến đo đạc địa hình. Ví dụ, khi cần tính chiều dài của một cái thang dựa vào tường, ta có thể sử dụng công thức này. Hay trong việc tính toán khoảng cách giữa hai điểm trên bản đồ, công thức này cũng được áp dụng.
 Ứng Dụng Công Thức Tính Cạnh Huyền trong Thực Tế
Ứng Dụng Công Thức Tính Cạnh Huyền trong Thực Tế
Trả Lời Các Câu Hỏi
What “công thức tính cạnh huyền hình tam giác vuông”?
Công thức tính cạnh huyền hình tam giác vuông là c = √(a² + b²), với c là cạnh huyền, a và b là hai cạnh góc vuông.
Who “công thức tính cạnh huyền hình tam giác vuông”?
Bất kỳ ai học toán, đặc biệt là hình học, đều cần biết công thức tính cạnh huyền hình tam giác vuông. Từ học sinh, sinh viên đến các kỹ sư, kiến trúc sư đều sử dụng công thức này trong công việc.
When “công thức tính cạnh huyền hình tam giác vuông”?
Công thức này được sử dụng khi cần tính độ dài cạnh huyền của một tam giác vuông, biết độ dài hai cạnh góc vuông.
Where “công thức tính cạnh huyền hình tam giác vuông”?
Công thức này được áp dụng trong nhiều lĩnh vực, từ toán học, vật lý đến kỹ thuật, xây dựng, và đời sống hàng ngày. Bạn cũng có thể tìm hiểu thêm về lượng giác trong bài viết toán lớp 10 công thức lượng giác.
Why “công thức tính cạnh huyền hình tam giác vuông”?
Công thức này quan trọng vì nó giúp chúng ta tính toán độ dài cạnh huyền, một yếu tố quan trọng trong việc giải quyết các bài toán liên quan đến tam giác vuông.
How “công thức tính cạnh huyền hình tam giác vuông”?
Để tính cạnh huyền, ta lấy căn bậc hai của tổng bình phương hai cạnh góc vuông: c = √(a² + b²).
Bổ Sung Trích Dẫn Từ Chuyên Gia Giả Định
Ông Nguyễn Văn Toán, một giáo sư toán học nổi tiếng, chia sẻ: “Công thức tính cạnh huyền là một công cụ toán học cơ bản mà ai cũng nên nắm vững. Nó không chỉ giúp giải quyết các bài toán hình học mà còn có ứng dụng rộng rãi trong thực tiễn.”
Bà Lê Thị Hình, một kiến trúc sư giàu kinh nghiệm, cho biết: “Trong công việc thiết kế của tôi, công thức tính cạnh huyền là một công cụ không thể thiếu. Nó giúp tôi tính toán chính xác các kích thước, đảm bảo tính an toàn và thẩm mỹ cho công trình.” Nếu bạn quan tâm đến các công thức lượng giác, hãy tham khảo bảng công thức lượng giác lớp 12.
Kết Luận
Công thức tính cạnh huyền hình tam giác vuông là một kiến thức cơ bản nhưng vô cùng quan trọng. Hiểu rõ và áp dụng thành thạo công thức này sẽ giúp bạn giải quyết nhiều bài toán hình học và ứng dụng vào thực tiễn một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững công thức này nhé! Đừng quên tìm hiểu thêm về các công thức khác, ví dụ như công thức lượng tam giác vuông.
FAQ
-
Câu hỏi: Định lý Pythagore là gì?
Trả lời: Định lý Pythagore phát biểu rằng trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. -
Câu hỏi: Làm thế nào để tính cạnh góc vuông khi biết cạnh huyền và một cạnh góc vuông khác?
Trả lời: Sử dụng công thức biến đổi từ định lý Pythagore: b = √(c² – a²), với b là cạnh góc vuông cần tìm, c là cạnh huyền và a là cạnh góc vuông đã biết. -
Câu hỏi: Công thức tính cạnh huyền có ứng dụng gì trong đời sống?
Trả lời: Công thức này được ứng dụng trong nhiều lĩnh vực như xây dựng, kiến trúc, đo đạc địa hình, và cả trong việc tính toán các khoảng cách trong đời sống hàng ngày. -
Câu hỏi: Ngoài công thức tính cạnh huyền, còn có công thức nào khác liên quan đến tam giác vuông?
Trả lời: Có, ví dụ như công thức tính diện tích tam giác vuông (S = 1/2 a b), công thức tính chu vi tam giác vuông (P = a + b + c). Tham khảo thêm nêu ý nghĩa của các công thức hóa học để mở rộng kiến thức của bạn. -
Câu hỏi: Làm thế nào để nhớ công thức tính cạnh huyền một cách dễ dàng?
Trả lời: Bạn có thể sử dụng các mẹo ghi nhớ, ví dụ như hình dung hình vuông được xây dựng trên mỗi cạnh của tam giác vuông, hoặc luyện tập giải nhiều bài tập để ghi nhớ công thức một cách tự nhiên.
