Công Thức Tính Cạnh Tam Giác Thường là một chủ đề quan trọng trong hình học, giúp chúng ta khám phá và giải quyết nhiều bài toán thực tiễn. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về các công thức tính cạnh của tam giác thường, từ cơ bản đến nâng cao, kèm theo ví dụ minh họa và câu hỏi thường gặp.
Định nghĩa Tam Giác Thường và Các Công Thức Cơ Bản
Tam giác thường là tam giác có ba cạnh và ba góc không nhất thiết phải bằng nhau. Để tính cạnh của tam giác thường, chúng ta có thể sử dụng một số công thức tùy thuộc vào dữ kiện bài toán cho sẵn. Một số công thức phổ biến bao gồm định lý cosine, định lý sin và công thức Heron. Ngay sau đây, chúng ta sẽ đi sâu vào chi tiết của từng công thức. Bạn có thể tham khảo thêm các công thức toán lớp 3 để nắm vững kiến thức cơ bản.
Định Lý Cosine
Định lý cosine cho phép ta tính cạnh của tam giác nếu biết hai cạnh còn lại và góc xen giữa chúng. Công thức được biểu diễn như sau: c² = a² + b² – 2ab*cos(C), trong đó a, b, c là độ dài ba cạnh của tam giác và C là góc đối diện với cạnh c.
 Minh họa Định Lý Cosine trong Tam Giác Thường
Minh họa Định Lý Cosine trong Tam Giác Thường
Định Lý Sin
Định lý sin thiết lập mối quan hệ giữa cạnh và góc đối diện trong tam giác. Công thức: a/sin(A) = b/sin(B) = c/sin(C) = 2R, với a, b, c là độ dài ba cạnh, A, B, C là các góc đối diện tương ứng, và R là bán kính đường tròn ngoại tiếp tam giác. Định lý sin hữu ích khi biết một cạnh và hai góc, hoặc hai cạnh và một góc không xen giữa. Bạn cũng có thể tìm hiểu thêm về các công thức trong tam giác cân để mở rộng kiến thức.
Công Thức Heron
Công thức Heron dùng để tính diện tích tam giác khi biết độ dài ba cạnh. Từ diện tích, ta có thể suy ra độ dài đường cao và sau đó tính cạnh bằng các công thức khác. Công thức Heron: S = sqrt(p(p-a)(p-b)(p-c)), với p là nửa chu vi tam giác (p = (a+b+c)/2).
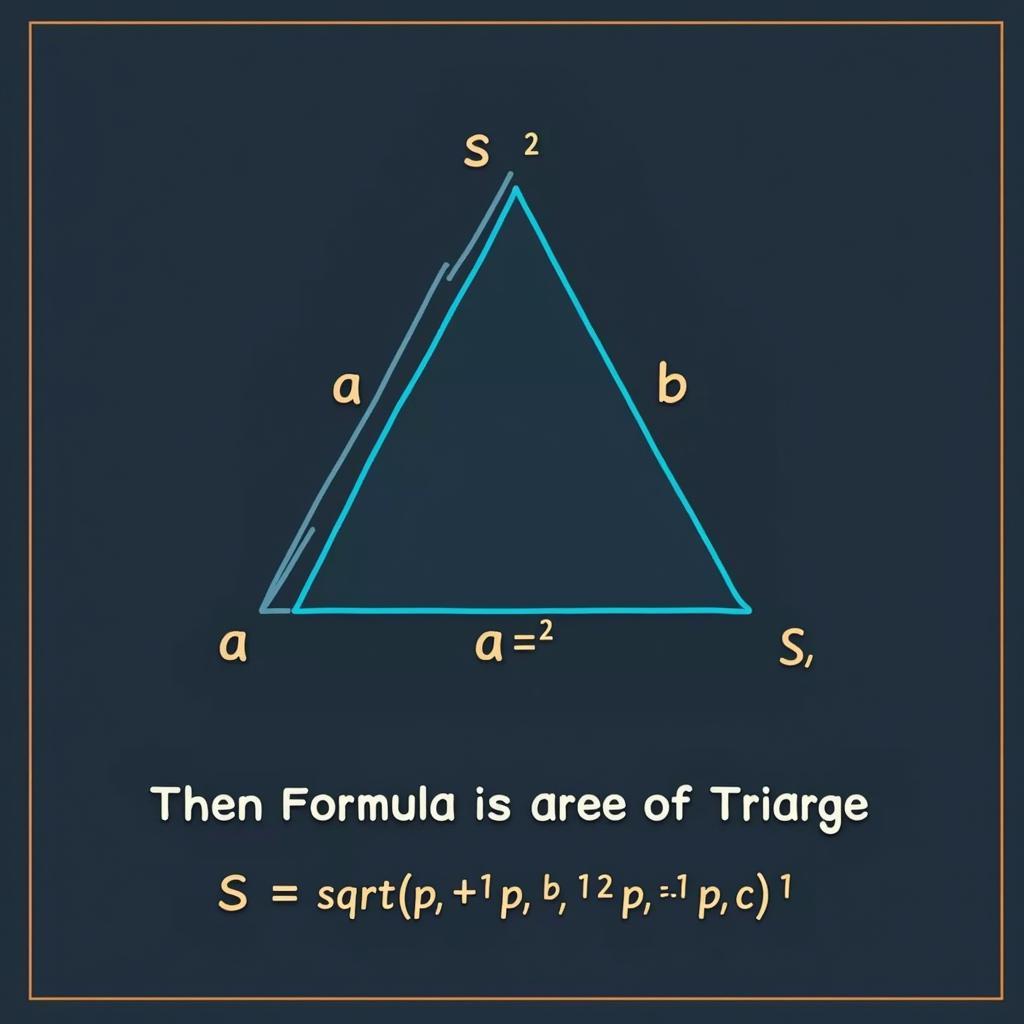 Minh họa Công Thức Heron tính Diện Tích Tam Giác
Minh họa Công Thức Heron tính Diện Tích Tam Giác
Các Trường Hợp Đặc Biệt và Bài Toán Ứng Dụng
Tam Giác Vuông
Trong tam giác vuông, ta có định lý Pythagoras: a² + b² = c², với a, b là hai cạnh góc vuông và c là cạnh huyền. Xem thêm công thức tính cạnh góc vuông trong tam giác vuông để hiểu rõ hơn.
Tam Giác Cân
Trong tam giác cân, hai cạnh bên bằng nhau. Điều này giúp đơn giản hóa việc tính toán.
Bài Toán Ứng Dụng
Công thức tính cạnh tam giác thường được ứng dụng rộng rãi trong đời sống, từ việc đo đạc đất đai, xây dựng, đến thiết kế đồ họa và kỹ thuật.
Trả Lời Các Câu Hỏi
What công thức tính cạnh tam giác thường?
Công thức tính cạnh tam giác thường bao gồm định lý cosine, định lý sin và công thức Heron.
Who sử dụng công thức tính cạnh tam giác thường?
Học sinh, sinh viên, kỹ sư, kiến trúc sư, và nhiều người khác sử dụng công thức này trong công việc và học tập.
When nên sử dụng công thức tính cạnh tam giác thường?
Khi cần tính toán độ dài cạnh của một tam giác thường, dựa trên các thông tin đã biết về tam giác đó.
Where áp dụng công thức tính cạnh tam giác thường?
Công thức này được áp dụng trong nhiều lĩnh vực, bao gồm toán học, vật lý, kỹ thuật, kiến trúc, và đo đạc.
Why cần học công thức tính cạnh tam giác thường?
Việc nắm vững công thức này giúp giải quyết nhiều bài toán hình học và ứng dụng thực tiễn.
How sử dụng công thức tính cạnh tam giác thường?
Xác định dữ kiện bài toán cho, chọn công thức phù hợp và thay số vào để tính toán. Tham khảo tổng hợp công thức toán trung học cơ sở để có cái nhìn tổng quan hơn.
 Ứng Dụng Công Thức Tính Cạnh Tam Giác
Ứng Dụng Công Thức Tính Cạnh Tam Giác
Chuyên Gia Nhận Định
Ông Nguyễn Văn A, Tiến sĩ Toán học, chia sẻ: “Nắm vững công thức tính cạnh tam giác thường là nền tảng quan trọng để học tốt hình học và giải quyết các bài toán thực tiễn.”
Bà Trần Thị B, Kỹ sư Xây dựng, cho biết: “Trong công việc của tôi, việc áp dụng công thức tính cạnh tam giác thường là rất cần thiết để tính toán chính xác các kích thước trong thiết kế công trình.”
Kết luận
Công thức tính cạnh tam giác thường là một công cụ hữu ích trong toán học và nhiều lĩnh vực khác. Hy vọng bài viết này đã cung cấp cho bạn kiến thức cần thiết về chủ đề này. Hãy tiếp tục tìm hiểu và luyện tập để thành thạo việc áp dụng các công thức.
FAQ
-
Câu hỏi: Định lý cosine là gì?
Trả lời: Định lý cosine là một công thức trong lượng giác liên hệ giữa các cạnh và góc của một tam giác. -
Câu hỏi: Định lý sin khác gì với định lý cosine?
Trả lời: Định lý sin liên hệ tỷ lệ giữa cạnh và sin của góc đối diện, trong khi định lý cosine liên hệ bình phương của một cạnh với hai cạnh còn lại và cosine của góc đối diện. -
Câu hỏi: Khi nào nên sử dụng công thức Heron?
Trả lời: Sử dụng công thức Heron khi biết độ dài ba cạnh của tam giác và muốn tính diện tích. -
Câu hỏi: Định lý Pythagoras áp dụng cho tam giác nào?
Trả lời: Định lý Pythagoras chỉ áp dụng cho tam giác vuông. -
Câu hỏi: Làm thế nào để nhớ các công thức tính cạnh tam giác thường?
Trả lời: Thực hành thường xuyên và hiểu rõ ý nghĩa của từng công thức là cách tốt nhất để ghi nhớ. Bạn có thể tham khảo thêm các công thức lượng giác cơ bản và nâng cao để củng cố kiến thức. -
Câu hỏi: Có tài liệu nào giúp tôi luyện tập thêm về công thức tính cạnh tam giác thường không?
Trả lời: Có rất nhiều sách giáo khoa và trang web cung cấp bài tập về chủ đề này. Bạn cũng có thể tìm kiếm các video hướng dẫn trực tuyến. -
Câu hỏi: Tôi có thể áp dụng công thức tính cạnh tam giác thường vào cuộc sống hàng ngày như thế nào?
Trả lời: Bạn có thể sử dụng nó để đo khoảng cách, tính diện tích đất, hoặc thậm chí là trong các trò chơi và hoạt động giải trí. -
Câu hỏi: Có phần mềm nào giúp tôi tính toán nhanh chóng các cạnh của tam giác không?
Trả lời: Có, nhiều phần mềm toán học và ứng dụng trực tuyến có thể giúp bạn tính toán các cạnh của tam giác một cách nhanh chóng và chính xác. -
Câu hỏi: Tôi cần biết gì trước khi học về công thức tính cạnh tam giác thường?
Trả lời: Bạn nên nắm vững kiến thức cơ bản về hình học, bao gồm các khái niệm về tam giác, góc, và các phép toán cơ bản. -
Câu hỏi: Làm thế nào để phân biệt tam giác thường với các loại tam giác khác?
Trả lời: Tam giác thường là tam giác không có đặc điểm đặc biệt nào như tam giác vuông (có một góc vuông), tam giác cân (có hai cạnh bằng nhau), hay tam giác đều (có ba cạnh bằng nhau).
