Công Thức V Chỏm Cầu là một khái niệm toán học quan trọng, thường gặp trong các bài toán tính thể tích. Bài viết này sẽ giúp bạn hiểu rõ về công thức này, cách áp dụng và những điều thú vị xoay quanh nó. công thức tính thể tích chỏm cầu
Hiểu Rõ Về Chỏm Cầu
Chỏm cầu là phần của hình cầu bị cắt bởi một mặt phẳng. Hình dung như khi bạn cắt một quả cam, mỗi phần được tạo ra có thể xem là một chỏm cầu. Việc tính toán thể tích của chỏm cầu có ứng dụng rộng rãi trong nhiều lĩnh vực, từ xây dựng đến thiết kế.
Thể tích chỏm cầu
Công Thức V Chỏm Cầu và Cách Áp Dụng
Công thức tính thể tích chỏm cầu (V) được biểu diễn như sau:
V = (πh^2/3) * (3R - h)Trong đó:
- V là thể tích chỏm cầu
- h là chiều cao của chỏm cầu
- R là bán kính của hình cầu
Để áp dụng công thức này, bạn cần xác định chiều cao (h) và bán kính (R) của chỏm cầu. Sau đó, thay các giá trị vào công thức và tính toán.
Ví Dụ Minh Họa
Giả sử bạn có một chỏm cầu với chiều cao h = 5cm và bán kính hình cầu R = 10cm. Thể tích của chỏm cầu sẽ được tính như sau:
V = (π * 5^2 / 3) * (3 * 10 - 5)
V ≈ 654.5 cm³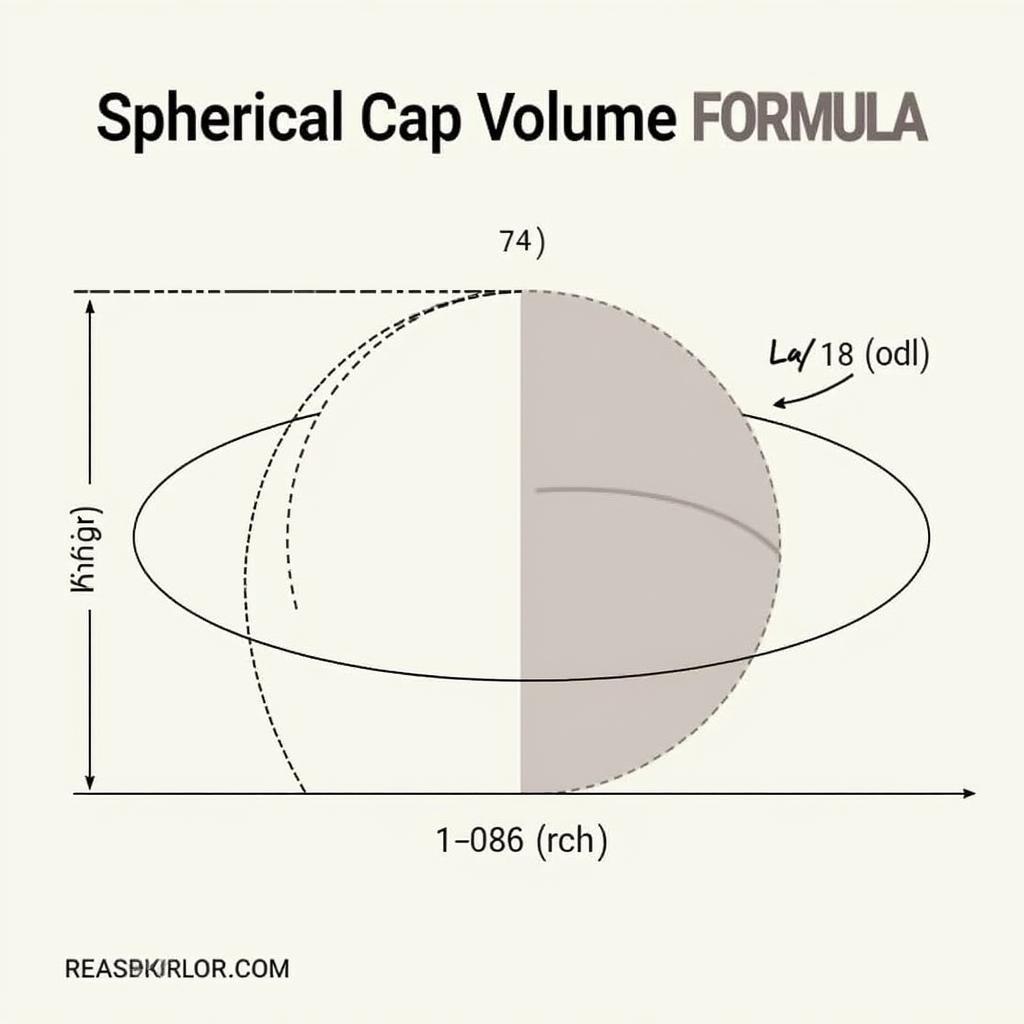
Áp dụng Công Thức V Chỏm Cầu
Công Thức Hình Chỏm Cầu trong Đời Sống
Công thức v chỏm cầu không chỉ là một khái niệm toán học khô khan mà còn có ứng dụng thực tiễn trong đời sống. Ví dụ, trong kiến trúc, công thức này được sử dụng để tính toán thể tích của mái vòm. Trong kỹ thuật, nó được dùng để tính thể tích của các bể chứa hình cầu. công thức hình chỏm cầu
What công thức v chỏm cầu?
Công thức v chỏm cầu là công thức tính thể tích của một phần hình cầu bị cắt bởi một mặt phẳng.
Who sử dụng công thức v chỏm cầu?
Kỹ sư, kiến trúc sư, nhà toán học và học sinh đều có thể sử dụng công thức này.
When nên sử dụng công thức v chỏm cầu?
Khi cần tính thể tích của một vật thể có hình dạng chỏm cầu.
Where áp dụng công thức v chỏm cầu?
Công thức này được áp dụng trong nhiều lĩnh vực, từ xây dựng, thiết kế đến toán học.
Why cần biết công thức v chỏm cầu?
Vì nó giúp chúng ta tính toán thể tích của các vật thể có hình dạng chỏm cầu, phục vụ cho nhiều mục đích khác nhau.
How sử dụng công thức v chỏm cầu?
Xác định chiều cao và bán kính, sau đó thay vào công thức V = (πh^2/3) * (3R - h) để tính toán.
Bảng Giá Chi Tiết (Ví dụ)
| Chiều cao (cm) | Bán kính (cm) | Thể tích (cm³) |
|---|---|---|
| 5 | 10 | 654.5 |
| 10 | 15 | 4712.4 |
| 15 | 20 | 14137.2 |
Ông Nguyễn Văn A, một kiến trúc sư giàu kinh nghiệm, chia sẻ: “Công thức v chỏm cầu là công cụ không thể thiếu trong công việc thiết kế của tôi. Nó giúp tôi tính toán chính xác thể tích của các mái vòm và các cấu trúc hình cầu khác.”
Ứng dụng thực tế chỏm cầu
Kết Luận
Công thức v chỏm cầu là một công cụ hữu ích cho việc tính toán thể tích. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về công thức này và cách áp dụng nó trong thực tế. các công thức giải nhanh toán 12 Hãy tiếp tục khám phá và áp dụng công thức v chỏm cầu trong học tập và công việc của bạn.
FAQ
1. Công thức v chỏm cầu là gì?
Công thức v chỏm cầu là công thức dùng để tính thể tích của một phần hình cầu bị cắt bởi một mặt phẳng.
2. Các yếu tố nào cần biết để tính thể tích chỏm cầu?
Bạn cần biết chiều cao của chỏm cầu (h) và bán kính của hình cầu (R).
3. Công thức tính thể tích chỏm cầu như thế nào?
Công thức là: V = (πh^2/3) * (3R – h)
4. Ứng dụng của công thức v chỏm cầu trong thực tế là gì?
Công thức này được ứng dụng trong kiến trúc, kỹ thuật, và nhiều lĩnh vực khác. công thức tính lãi cộng dồn
5. Tôi có thể tìm thấy thêm thông tin về công thức này ở đâu?
Bạn có thể tìm thấy thêm thông tin trên các trang web toán học hoặc sách giáo khoa.
6. Độ phức tạp của việc tính toán công thức này như thế nào?
Việc tính toán khá đơn giản nếu bạn có đủ thông tin về chiều cao và bán kính.
7. Có công cụ nào hỗ trợ tính toán nhanh công thức này không?
Có nhiều máy tính trực tuyến và phần mềm toán học có thể giúp bạn tính toán nhanh chóng.
8. Công thức này có liên quan gì đến các công thức hình học khác không?
Có, nó liên quan đến công thức tính thể tích hình cầu và hình nón. công thức vật lý 10 nâng cao
9. Làm thế nào để nhớ công thức này dễ dàng?
Bạn có thể viết công thức ra giấy nhiều lần hoặc sử dụng các phương pháp ghi nhớ khác.
10. Có ví dụ thực tế nào về ứng dụng của công thức này không?
Tính toán thể tích của mái vòm trong kiến trúc là một ví dụ điển hình.