Công Thức Hình Lăng Trụ là nền tảng để tính toán các đại lượng liên quan đến hình học không gian này. Bài viết này sẽ đi sâu vào chi tiết về các công thức hình lăng trụ, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và áp dụng vào thực tế.
Công Thức Tính Diện Tích Hình Lăng Trụ
Diện tích hình lăng trụ được chia thành hai loại chính: diện tích xung quanh và diện tích toàn phần.
Diện tích Xung Quanh
Diện tích xung quanh của hình lăng trụ được tính bằng chu vi đáy nhân với chiều cao. Công thức chung là:
- *Sxq = P h**
Trong đó:
- Sxq: Diện tích xung quanh
- P: Chu vi đáy
- h: Chiều cao
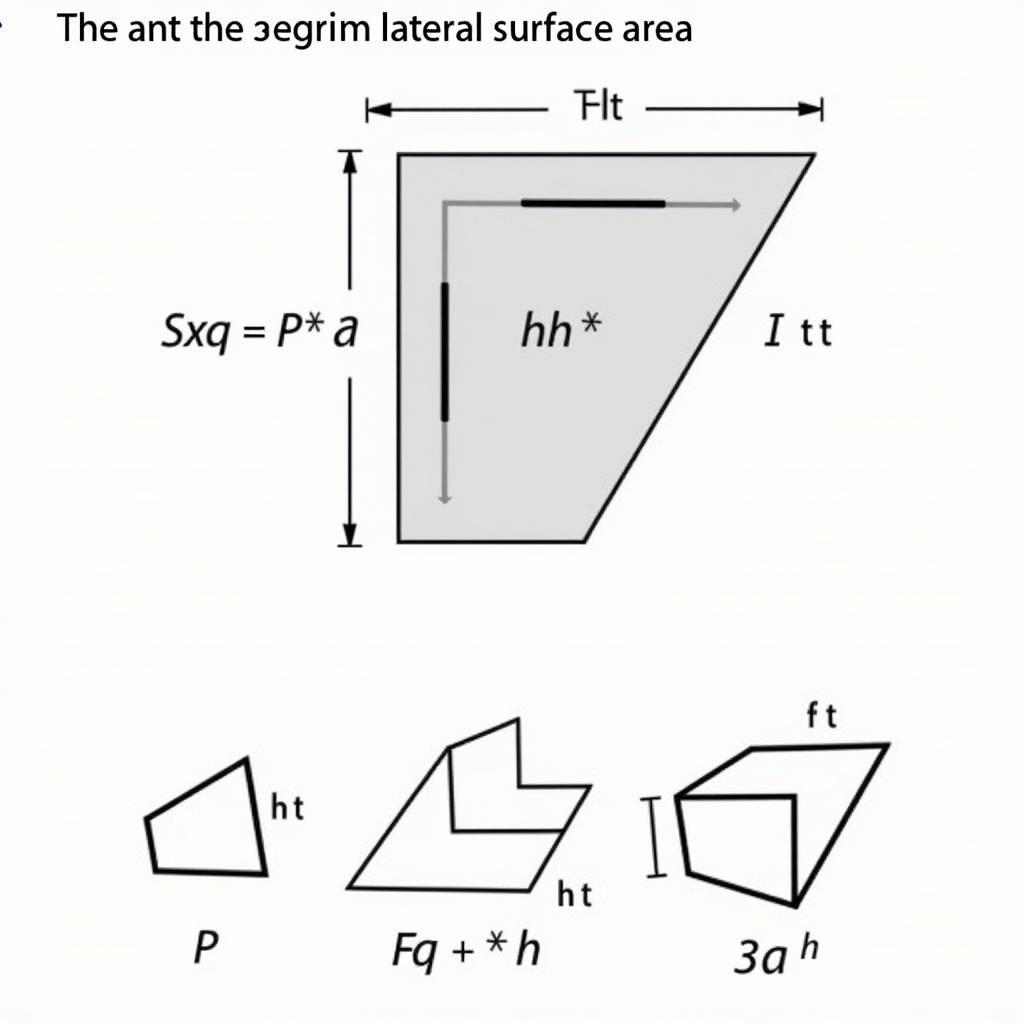Diện tích xung quanh hình lăng trụ
Diện tích Toàn Phần
Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy. Công thức chung là:
- *Stp = Sxq + 2 Sđ**
Trong đó:
- Stp: Diện tích toàn phần
- Sxq: Diện tích xung quanh
- Sđ: Diện tích đáy
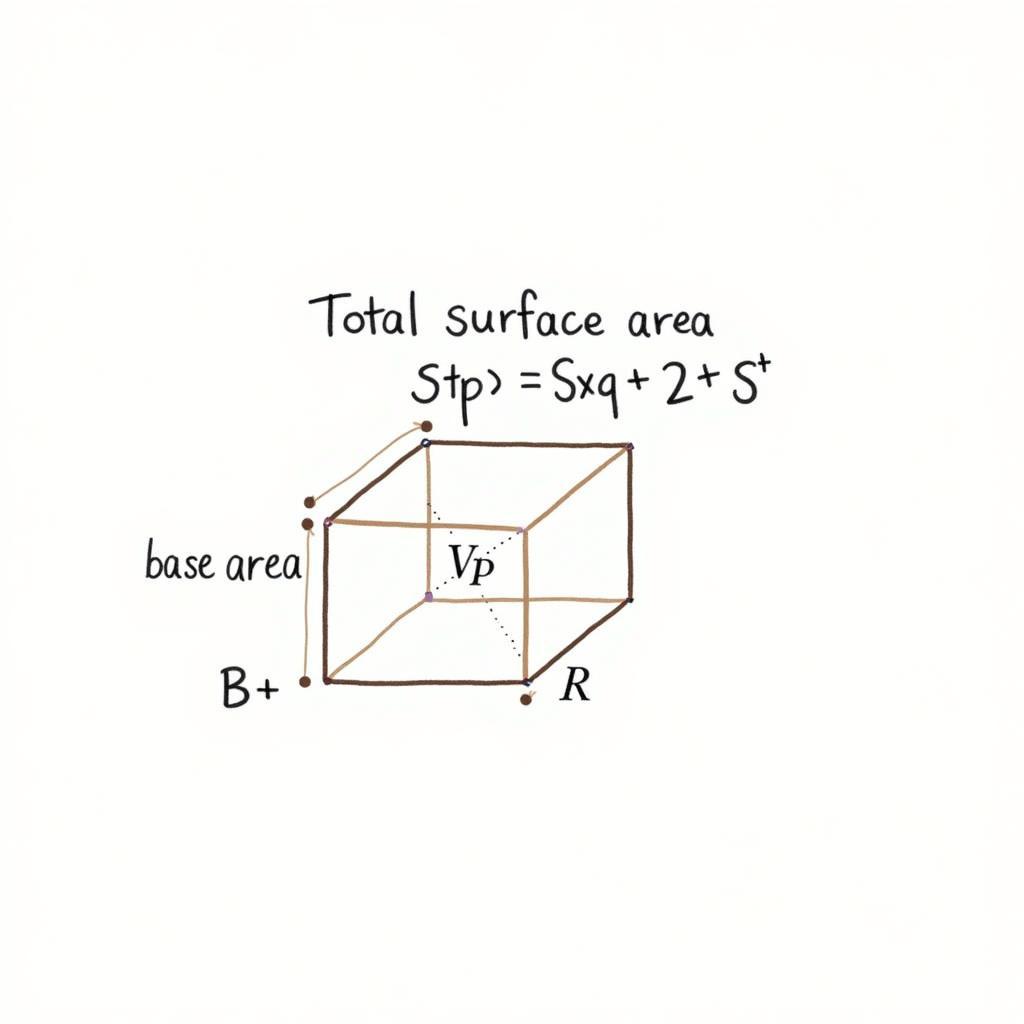Diện tích toàn phần hình lăng trụ
Công Thức Tính Thể Tích Hình Lăng Trụ
Thể tích hình lăng trụ được tính bằng diện tích đáy nhân với chiều cao. Công thức chung là:
- *V = Sđ h**
Trong đó:
- V: Thể tích
- Sđ: Diện tích đáy
- h: Chiều cao
Ví dụ, nếu bạn muốn bánh mì chuối công thức và muốn tính thể tích khuôn bánh hình lăng trụ, bạn có thể áp dụng công thức này.
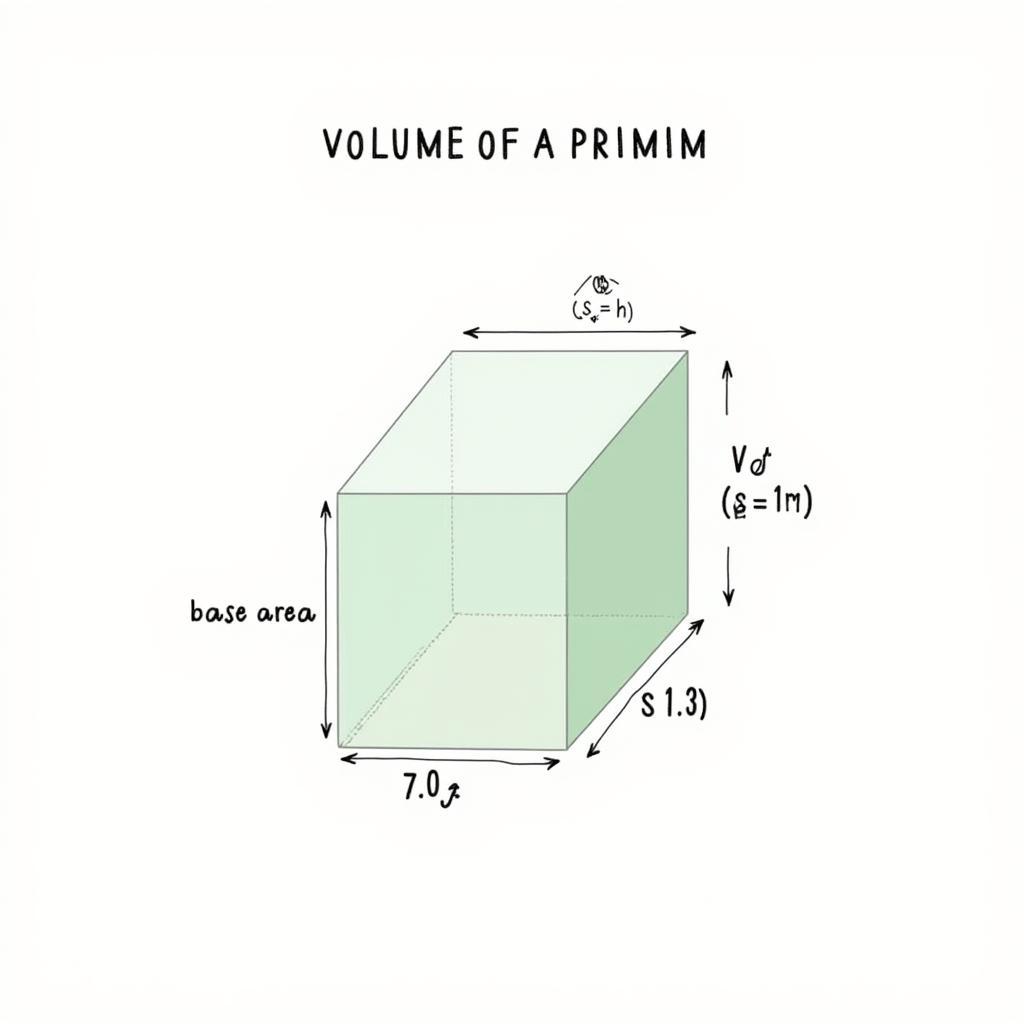Thể tích hình lăng trụ
Trả Lời Các Câu Hỏi
What “công thức hình lăng trụ”
Công thức hình lăng trụ bao gồm công thức tính diện tích (xung quanh, toàn phần) và thể tích.
Who “công thức hình lăng trụ”
Học sinh, sinh viên, kỹ sư, kiến trúc sư, và bất kỳ ai làm việc với hình học không gian đều sử dụng công thức hình lăng trụ.
When “công thức hình lăng trụ”
Công thức hình lăng trụ được sử dụng khi cần tính toán diện tích hoặc thể tích của hình lăng trụ.
Where “công thức hình lăng trụ”
Công thức hình lăng trụ được áp dụng trong nhiều lĩnh vực, từ toán học đến xây dựng, thiết kế, và cả trong cuộc sống hàng ngày.
Why “công thức hình lăng trụ”
Công thức hình lăng trụ giúp chúng ta hiểu rõ hơn về hình học không gian và giải quyết các bài toán thực tế liên quan đến hình lăng trụ.
How “công thức hình lăng trụ”
Áp dụng công thức hình lăng trụ bằng cách xác định các đại lượng cần thiết (chu vi đáy, diện tích đáy, chiều cao) và thay vào công thức tương ứng.
Bảng Giá Chi Tiết (Ví dụ ứng dụng trong xây dựng)
| Loại Vật Liệu | Đơn Giá (VNĐ/m3) |
|---|---|
| Gạch | 2.000.000 |
| Xi măng | 1.500.000 |
| Cát | 500.000 |
Nếu bạn cần công thức tính khối lượng san lấp mặt bằng hình lăng trụ, kiến thức về thể tích sẽ rất hữu ích.
Trích dẫn từ Chuyên gia
- Ông Nguyễn Văn A, kiến trúc sư hàng đầu tại Việt Nam, cho biết: “Nắm vững công thức hình lăng trụ là điều kiện tiên quyết cho bất kỳ ai muốn theo đuổi ngành kiến trúc.”
- Bà Trần Thị B, giáo viên Toán THCS, chia sẻ: “Việc hiểu rõ công thức hình lăng trụ giúp học sinh phát triển tư duy hình học không gian và giải quyết các bài toán một cách hiệu quả.”
Kết luận
Tóm lại, công thức hình lăng trụ là kiến thức cơ bản và quan trọng trong hình học không gian. Hiểu rõ và áp dụng thành thạo các công thức này sẽ giúp bạn giải quyết nhiều bài toán thực tế. công thức tính hình lăng trụ được ứng dụng rộng rãi trong nhiều lĩnh vực.
FAQ
-
Câu hỏi: Công thức tính diện tích xung quanh của hình lăng trụ là gì?
Trả lời: Sxq = P * h (P là chu vi đáy, h là chiều cao). -
Câu hỏi: Làm thế nào để tính thể tích của hình lăng trụ tam giác?
Trả lời: V = (1/2 a h) * H (a là cạnh đáy tam giác, h là chiều cao tam giác, H là chiều cao lăng trụ). -
Câu hỏi: Công thức tính diện tích toàn phần của hình lăng trụ là gì?
Trả lời: Stp = Sxq + 2 * Sđ (Sxq là diện tích xung quanh, Sđ là diện tích đáy). -
Câu hỏi: Ứng dụng của công thức hình lăng trụ trong đời sống là gì?
Trả lời: Tính toán thể tích bể nước, khối lượng vật liệu xây dựng, thiết kế các vật dụng hình lăng trụ… -
Câu hỏi: Làm thế nào để nhớ các công thức hình lăng trụ một cách dễ dàng?
Trả lời: Thực hành thường xuyên và vẽ hình minh họa sẽ giúp bạn ghi nhớ công thức nhanh hơn. -
Câu hỏi: Có công cụ nào hỗ trợ tính toán hình lăng trụ không?
Trả lời: Có nhiều phần mềm và ứng dụng trực tuyến hỗ trợ tính toán hình học, bao gồm cả hình lăng trụ. -
Câu hỏi: Tôi cần tìm hiểu thêm về công thức tính điện trở theo tiết diện ở đâu?
Trả lời: Bạn có thể tìm hiểu thêm về công thức tính điện trở theo tiết diện tại website taixiu.shop. -
Câu hỏi: Công thức tính hao hụt được tính như thế nào?
Trả lời: Bạn có thể tham khảo công thức tính hao hụt tại website taixiu.shop. -
Câu hỏi: Có tài liệu nào hướng dẫn chi tiết về công thức hình lăng trụ không?
Trả lời: Có rất nhiều sách giáo khoa và tài liệu trực tuyến về hình học không gian cung cấp thông tin chi tiết về công thức hình lăng trụ. -
Câu hỏi: Tôi gặp khó khăn khi áp dụng công thức hình lăng trụ, tôi có thể tìm sự giúp đỡ ở đâu?
Trả lời: Bạn có thể hỏi giáo viên, bạn bè, hoặc tham gia các diễn đàn học tập trực tuyến để được giải đáp thắc mắc.