Công thức tan, một khái niệm toán học quen thuộc, xuất hiện từ những bài học đầu tiên về lượng giác. Nhưng liệu bạn đã bao giờ tự hỏi, ẩn sau những con số và ký hiệu khô khan ấy, liệu có một vẻ đẹp nào khác, một sự lãng mạn nào khác được thể hiện qua những vần thơ?
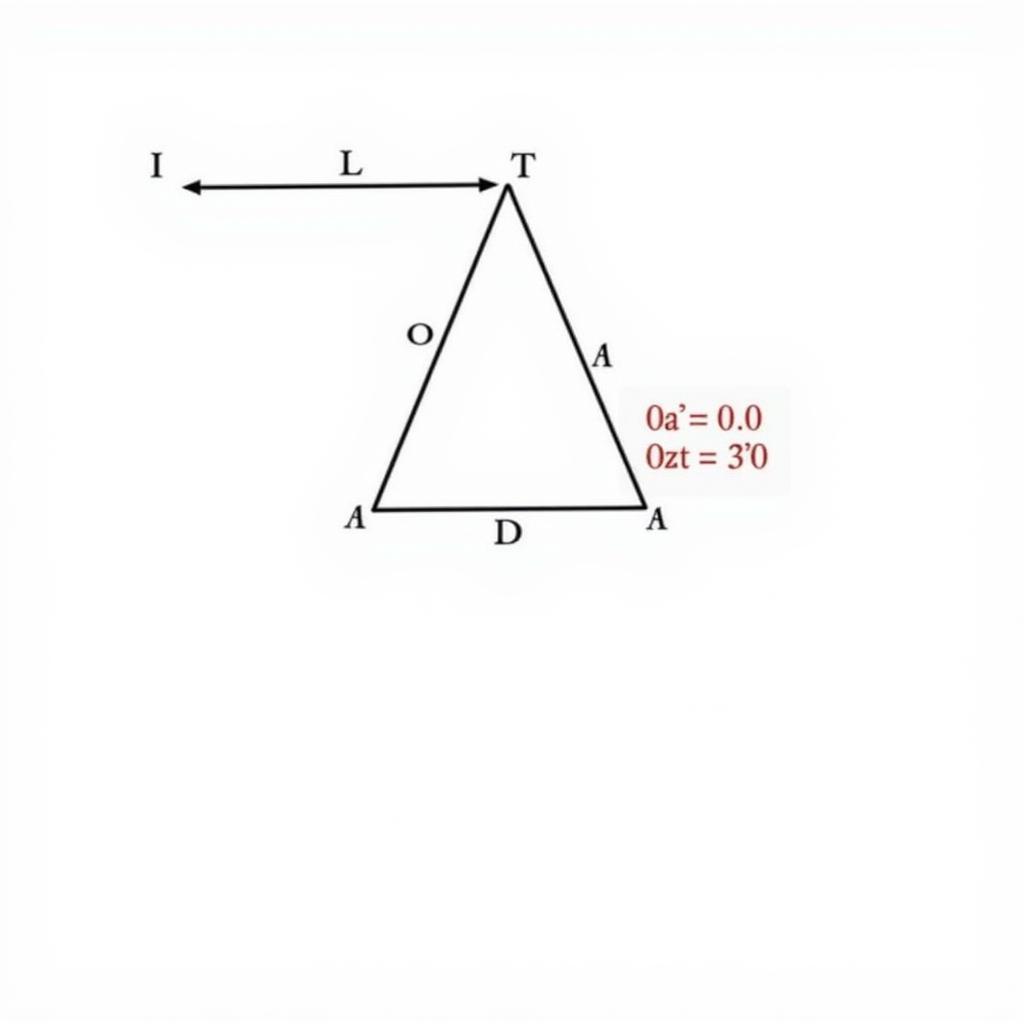 Công thức tan trong tam giác vuông
Công thức tan trong tam giác vuông
Khám Phá Vẻ Đẹp Của Công Thức Tan Qua Lăng Kính Thơ Ca
Công thức tan, được định nghĩa là tỷ số giữa cạnh đối và cạnh kề của một góc nhọn trong tam giác vuông, không chỉ đơn thuần là một công thức toán học. Nó là chìa khóa để mở ra cánh cửa vào thế giới của các góc và cạnh, giúp chúng ta khám phá mối quan hệ giữa chúng. Việc hiểu rõ công thức tan sẽ giúp bạn giải quyết nhiều bài toán hình học phức tạp. Bạn cũng có thể tìm hiểu thêm về đặt công thức tính trong excel.
Tan Trong Tam Giác Vuông
Trong hình học, công thức tan đóng vai trò quan trọng trong việc tính toán các cạnh và góc của tam giác vuông. Nó cho phép chúng ta liên kết một góc nhọn với tỷ số giữa hai cạnh của tam giác. Từ đó, ta có thể xác định được độ dài các cạnh hoặc số đo góc chưa biết.
 Ứng dụng công thức tan trong thực tế
Ứng dụng công thức tan trong thực tế
Công Thức Tan và Những Bài Thơ Số
Những con số và ký hiệu toán học, tưởng chừng khô khan, lại có thể trở thành nguồn cảm hứng cho những bài thơ đầy chất toán. Công thức tan cũng không ngoại lệ. Hãy cùng chiêm ngưỡng một vài bài thơ số được lấy cảm hứng từ công thức tan:
- Cạnh đối chia cạnh kề,
- Tan góc hiện ra, ồ lạ kỳ.
Hay:
- Góc nhọn trong tam giác vuông,
- Đối chia kề, tan hiện hữu.
Tìm Hiểu Sâu Hơn Về Công Thức Tan
Công thức tan không chỉ giới hạn trong tam giác vuông. Nó còn được mở rộng ra cho các góc bất kỳ trong đường tròn lượng giác. Việc tìm hiểu sâu hơn về công thức tan trong đường tròn lượng giác sẽ giúp bạn hiểu rõ hơn về bản chất và ứng dụng của nó. Nếu bạn quan tâm đến các bài tập thực hành, hãy tham khảo bài tập cơ bản về công thức nghiệm violet.
 Biểu diễn công thức tan trên đường tròn lượng giác
Biểu diễn công thức tan trên đường tròn lượng giác
Trả Lời Các Câu Hỏi
- What Bài Thơ Về Công Thức Tan? Bài thơ về công thức tan là những sáng tác thơ sử dụng hình ảnh và ngôn ngữ toán học để diễn tả vẻ đẹp và ý nghĩa của công thức tan.
- Who sáng tác bài thơ về công thức tan? Bài thơ về công thức tan có thể được sáng tác bởi bất kỳ ai yêu thích toán học và thơ ca.
- When nên sử dụng công thức tan? Công thức tan được sử dụng khi cần tính toán các cạnh và góc trong tam giác vuông, hoặc khi làm việc với đường tròn lượng giác.
- Where tìm thấy công thức tan? Công thức tan được tìm thấy trong sách giáo khoa toán học, các tài liệu tham khảo về lượng giác, và trên internet.
- Why công thức tan quan trọng? Công thức tan quan trọng vì nó là một công cụ hữu ích trong việc giải quyết các bài toán hình học và lượng giác.
- How áp dụng công thức tan? Để áp dụng công thức tan, cần xác định cạnh đối và cạnh kề của góc nhọn trong tam giác vuông, sau đó tính tỷ số giữa chúng.
Kết Luận
Công thức tan, tuy đơn giản nhưng lại chứa đựng nhiều điều thú vị. Qua lăng kính thơ ca, ta có thể thấy được vẻ đẹp tiềm ẩn của công thức tan, cũng như sự kết nối giữa toán học và nghệ thuật. Bạn cũng đừng quên tìm hiểu bí kíp thức tỉnh võ công mua ở đâu nếu bạn yêu thích võ thuật.
FAQ
-
Câu hỏi 1: Làm thế nào để nhớ công thức tan?
-
Trả lời: Có nhiều cách để nhớ công thức tan, ví dụ như sử dụng câu thần chú “Đối chia kề”.
-
Câu hỏi 2: Công thức tan có liên quan gì đến sin và cos?
-
Trả lời: Tan của một góc bằng sin của góc đó chia cho cos của góc đó.
-
Câu hỏi 3: Ứng dụng của công thức tan trong đời sống là gì?
-
Trả lời: Công thức tan được ứng dụng trong nhiều lĩnh vực, ví dụ như đo đạc, xây dựng, và định vị. Bạn có thể tham khảo diện tích lăng trụ công thức để tìm hiểu thêm về ứng dụng của toán học trong tính toán diện tích.
-
Câu hỏi 4: Làm thế nào để tính tan của một góc nếu biết sin và cos của góc đó?
-
Trả lời: Chia sin của góc cho cos của góc.
-
Câu hỏi 5: Có công cụ nào giúp tính toán công thức tan nhanh chóng không?
-
Trả lời: Có, bạn có thể sử dụng máy tính hoặc các ứng dụng tính toán trực tuyến. Công thức tính lãi suất lũy tiến cũng là một ví dụ về ứng dụng của công cụ tính toán trong tài chính.
