Công thức tính độ dài trong Oxy là một công cụ quan trọng trong hình học giải tích. Nó cho phép chúng ta tính toán khoảng cách giữa hai điểm trên mặt phẳng tọa độ Oxy một cách chính xác và nhanh chóng. Bài viết này sẽ đi sâu vào chứng minh công thức này, đồng thời khám phá các ứng dụng của nó trong thực tế.
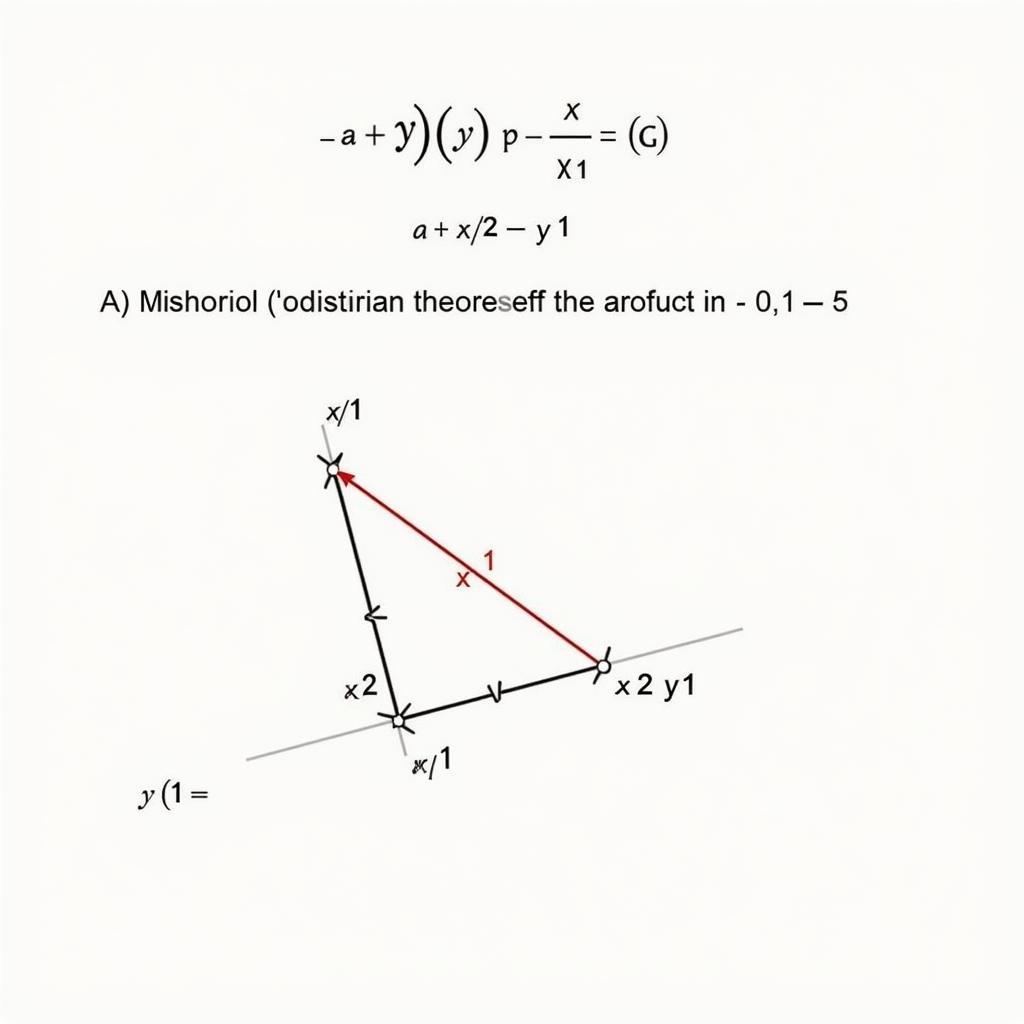 Chứng minh công thức tính độ dài trong Oxy
Chứng minh công thức tính độ dài trong Oxy
Định nghĩa Hệ Tọa Độ Oxy và Độ Dài
Hệ tọa độ Oxy là một hệ trục tọa độ vuông góc, gồm hai trục Ox và Oy giao nhau tại gốc tọa độ O. Mỗi điểm trên mặt phẳng được biểu diễn bởi một cặp số (x, y), gọi là tọa độ của điểm đó. Độ dài, hay khoảng cách giữa hai điểm, chính là độ lớn của đoạn thẳng nối hai điểm đó.
Chứng Minh Công Thức Tính Độ Dài
Giả sử ta có hai điểm A(x₁, y₁) và B(x₂, y₂) trên mặt phẳng Oxy. Để tính độ dài đoạn thẳng AB, ta dựng một tam giác vuông ABC, với C(x₂, y₁). Độ dài cạnh AC là |x₂ – x₁| và độ dài cạnh BC là |y₂ – y₁|. Theo định lý Pythagore, ta có:
AB² = AC² + BC²
AB² = (x₂ – x₁)² + (y₂ – y₁)²
AB = √[(x₂ – x₁)² + (y₂ – y₁)²]
Đây chính là công thức tính độ dài trong Oxy.
Ứng Dụng Của Công Thức Tính Độ Dài
Công thức tính độ dài có rất nhiều ứng dụng trong toán học và các lĩnh vực khác. Ví dụ, ta có thể sử dụng công thức này để:
- Tính chu vi và diện tích của các hình học phẳng.
- Xác định vị trí tương đối của các điểm và đường thẳng.
- Giải quyết các bài toán liên quan đến hình học không gian.
- Trong chẩn đoán thiếu máu công thức máu, việc tính toán khoảng cách giữa các điểm dữ liệu cũng rất quan trọng.
Trả Lời Các Câu Hỏi:
- What “chứng minh công thức tính độ dài trong oxy”?: Chứng minh công thức tính độ dài trong Oxy là việc sử dụng định lý Pythagore để chứng minh công thức √[(x₂ – x₁)² + (y₂ – y₁)²].
- Who “chứng minh công thức tính độ dài trong oxy”?: Học sinh, sinh viên, và bất kỳ ai quan tâm đến toán học đều có thể tìm hiểu và chứng minh công thức này.
- When “chứng minh công thức tính độ dài trong oxy”?: Công thức này thường được học ở bậc trung học cơ sở.
- Where “chứng minh công thức tính độ dài trong oxy”?: Công thức này được chứng minh và áp dụng trong hình học giải tích trên mặt phẳng Oxy.
- Why “chứng minh công thức tính độ dài trong oxy”?: Việc chứng minh giúp hiểu rõ bản chất của công thức và cách áp dụng nó.
- How “chứng minh công thức tính độ dài trong oxy”?: Công thức được chứng minh bằng cách sử dụng định lý Pythagore trên một tam giác vuông được tạo thành từ hai điểm đã cho.
Trích dẫn từ chuyên gia
Theo Tiến sĩ Nguyễn Văn A, chuyên gia toán học tại Đại học Quốc gia Hà Nội: “Công thức tính độ dài trong Oxy là một công cụ cơ bản nhưng vô cùng mạnh mẽ. Nó là nền tảng cho nhiều khái niệm phức tạp hơn trong hình học giải tích.”
Ông Lê Văn B, giảng viên toán tại trường THPT Chuyên Hà Nội – Amsterdam, cũng cho biết: “Việc nắm vững công thức này sẽ giúp học sinh dễ dàng tiếp cận và giải quyết các bài toán hình học phức tạp hơn.” công thức tính nhanh este cũng là một ví dụ về việc áp dụng công thức một cách hiệu quả.
Kết luận
Công thức tính độ dài trong Oxy là một công cụ quan trọng trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực. Hiểu rõ cách chứng minh và áp dụng công thức này sẽ giúp bạn giải quyết nhiều bài toán khác nhau một cách hiệu quả. công thức cyanua và công thức nhuộm nâu tro cũng là những ví dụ về việc áp dụng công thức trong các lĩnh vực khác nhau. Hãy luyện tập và khám phá thêm về những ứng dụng thú vị của nó. công thức cấu tạo c2h6o cũng liên quan đến việc biểu diễn cấu trúc phân tử trên mặt phẳng tọa độ.
FAQ
-
Nêu Câu Hỏi: Định lý Pythagore là gì?
Trả Lời Chi tiết Câu Hỏi: Định lý Pythagore phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. -
Nêu Câu Hỏi: Làm thế nào để nhớ công thức tính độ dài trong Oxy?
Trả Lời Chi tiết Câu Hỏi: Hãy liên tưởng đến định lý Pythagore và hình dung tam giác vuông được tạo thành từ hai điểm. -
Nêu Câu Hỏi: Có cách nào khác để tính độ dài trong Oxy không?
Trả Lời Chi tiết Câu Hỏi: Về cơ bản, công thức dựa trên định lý Pythagore là cách phổ biến và hiệu quả nhất. -
Nêu Câu Hỏi: Công thức tính độ dài có áp dụng cho không gian ba chiều không?
Trả Lời Chi tiết Câu Hỏi: Có, công thức được mở rộng cho không gian ba chiều với thêm tọa độ z. -
Nêu Câu Hỏi: Tôi có thể tìm tài liệu tham khảo về công thức tính độ dài ở đâu?
Trả Lời Chi tiết Câu Hỏi: Bạn có thể tìm thấy thông tin trong sách giáo khoa toán học, hoặc trên các trang web học tập trực tuyến. -
Nêu Câu Hỏi: Ứng dụng của công thức tính độ dài trong đời sống là gì?
Trả Lời Chi tiết Câu Hỏi: Công thức này được sử dụng trong nhiều lĩnh vực, từ định vị GPS đến thiết kế đồ họa. -
Nêu Câu Hỏi: Độ dài có luôn là một số dương không?
Trả Lời Chi tiết Câu Hỏi: Đúng, độ dài luôn là một số không âm. -
Nêu Câu Hỏi: Làm thế nào để tính khoảng cách giữa một điểm và một đường thẳng?
Trả Lời Chi tiết Câu Hỏi: Có công thức riêng để tính khoảng cách giữa một điểm và một đường thẳng, liên quan đến công thức tính độ dài. -
Nêu Câu Hỏi: Tọa độ của một điểm có thể là số âm không?
Trả Lời Chi tiết Câu Hỏi: Có, tọa độ của một điểm có thể là số âm, dương hoặc bằng 0. -
Nêu Câu Hỏi: Tại sao cần phải học chứng minh công thức tính độ dài?
Trả Lời Chi tiết Câu Hỏi: Việc chứng minh giúp hiểu sâu hơn về công thức và phát triển tư duy toán học.
