Công Thức Cạnh Huyền Tam Giác Vuông là một trong những công thức toán học cơ bản nhất, nhưng cũng vô cùng quan trọng. Nó không chỉ là nền tảng cho hình học phẳng mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống. Bài viết này sẽ giúp bạn khám phá mọi khía cạnh của công thức này, từ định nghĩa, cách chứng minh, đến ứng dụng thực tiễn.
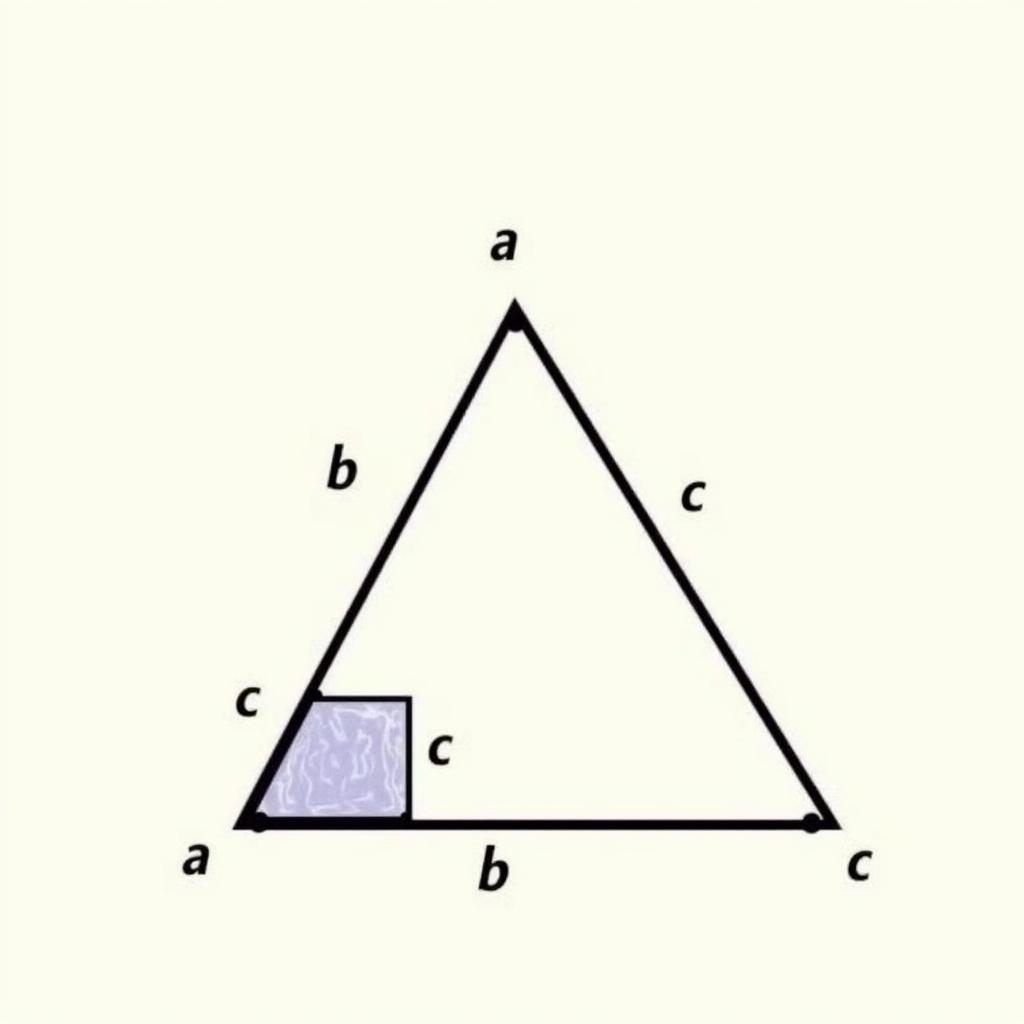 Minh họa Định Lý Pytago trên tam giác vuông
Minh họa Định Lý Pytago trên tam giác vuông
Định Nghĩa Công Thức Cạnh Huyền Tam Giác Vuông
Công thức cạnh huyền tam giác vuông, hay còn gọi là định lý Pytago, phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Nói cách khác, nếu gọi độ dài cạnh huyền là c và độ dài hai cạnh góc vuông là a và b, thì ta có công thức: a² + b² = c². Công thức này được đặt theo tên nhà toán học và triết học Hy Lạp cổ đại Pythagoras, người được cho là đã chứng minh định lý này.
Trong học toán hình lớp 8, chúng ta đã được làm quen với công thức toán hình lớp 8. Việc nắm vững các công thức này là nền tảng để hiểu rõ hơn về định lý Pytago.
Chứng Minh Công Thức Cạnh Huyền
Có rất nhiều cách chứng minh định lý Pytago. Một trong những cách chứng minh trực quan nhất là sử dụng hình vuông. Ta có thể vẽ một hình vuông lớn với cạnh bằng a + b. Bên trong hình vuông lớn này, ta vẽ bốn tam giác vuông giống nhau với hai cạnh góc vuông là a và b. Diện tích hình vuông lớn bằng (a + b)². Diện tích bốn tam giác vuông bằng 2ab. Diện tích hình vuông nhỏ còn lại (hình vuông được tạo bởi bốn cạnh huyền của bốn tam giác vuông) bằng c². Từ đó, ta có (a + b)² = 2ab + c², hay a² + 2ab + b² = 2ab + c². Rút gọn, ta được a² + b² = c².
Ứng Dụng Của Công Thức Cạnh Huyền Tam Giác Vuong
Công thức cạnh huyền tam giác vuông có rất nhiều ứng dụng trong thực tế. Ví dụ, trong xây dựng, người ta sử dụng công thức này để tính toán độ dài của các thanh giằng, độ cao của mái nhà, và khoảng cách giữa các điểm. Trong định vị, công thức này được sử dụng để tính toán khoảng cách giữa hai điểm trên bản đồ. Trong vật lý, công thức này được sử dụng để tính toán độ lớn của các vectơ.
 Ứng dụng Công Thức Cạnh Huyền trong Xây Dựng
Ứng dụng Công Thức Cạnh Huyền trong Xây Dựng
Việc hiểu rõ về công thức của đường tròn cũng giúp ích rất nhiều trong việc áp dụng định lý Pytago trong các bài toán hình học phức tạp hơn.
Trả Lời Các Câu Hỏi
What Công Thức Cạnh Huyền Tam Giác Vuông?
Công thức cạnh huyền tam giác vuông, hay định lý Pytago, phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông (a² + b² = c²).
Who Công Thức Cạnh Huyền Tam Giác Vuông?
Định lý này được đặt theo tên nhà toán học và triết học Hy Lạp cổ đại Pythagoras.
When Công Thức Cạnh Huyền Tam Giác Vuông?
Định lý Pytago đã được biết đến từ thời cổ đại, nhưng Pythagoras được cho là người đầu tiên chứng minh nó một cách toán học.
Where Công Thức Cạnh Huyền Tam Giác Vuông?
Công thức này được áp dụng trong rất nhiều lĩnh vực, từ toán học, vật lý, đến xây dựng, định vị, và nhiều lĩnh vực khác.
Why Công Thức Cạnh Huyền Tam Giác Vuông?
Công thức này quan trọng vì nó thiết lập mối quan hệ giữa các cạnh của một tam giác vuông, cho phép chúng ta tính toán độ dài của một cạnh bất kỳ khi biết độ dài của hai cạnh còn lại.
How Công Thức Cạnh Huyền Tam Giác Vuông?
Để áp dụng công thức, ta cần xác định đâu là cạnh huyền (cạnh đối diện với góc vuông) và hai cạnh góc vuông. Sau đó, ta thay các giá trị vào công thức a² + b² = c² để tính toán.
Trích Dẫn Chuyên Gia
GS.TS Nguyễn Văn A, chuyên gia toán học hàng đầu Việt Nam, cho biết: “Định lý Pytago không chỉ là một công thức toán học đơn thuần, mà còn là một minh chứng cho vẻ đẹp và sự hài hòa của toán học.”
TS. Lê Thị B, giảng viên Đại học Sư Phạm Hà Nội, chia sẻ: “Việc hiểu và áp dụng thành thạo định lý Pytago là nền tảng quan trọng cho việc học tập và nghiên cứu các lĩnh vực khoa học kỹ thuật.”
Kỹ sư Trần Văn C, chuyên gia xây dựng, nhận định: “Định lý Pytago là công cụ không thể thiếu trong công việc thiết kế và xây dựng của chúng tôi. Nó giúp chúng tôi tính toán chính xác các kích thước và đảm bảo sự ổn định của công trình.”
Kết luận
Công thức cạnh huyền tam giác vuông, hay định lý Pytago, là một công thức toán học cơ bản nhưng vô cùng quan trọng. Nó có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống. Hiểu rõ và áp dụng thành thạo công thức này sẽ giúp bạn giải quyết nhiều bài toán thực tế và nâng cao hiểu biết về toán học. Hãy cùng tiếp tục khám phá và ứng dụng công thức này trong cuộc sống hàng ngày. Có thể bạn sẽ thấy hữu ích khi tham khảo thêm về bảng công thức lượng giác cần nhớ và công thức về lăng kính. Chúng cũng có những ứng dụng đáng kinh ngạc trong thực tế.
FAQ
-
Câu hỏi: Định lý Pytago áp dụng cho tam giác nào?
Trả lời: Định lý Pytago chỉ áp dụng cho tam giác vuông. -
Câu hỏi: Làm thế nào để xác định cạnh huyền trong tam giác vuông?
Trả lời: Cạnh huyền là cạnh đối diện với góc vuông. -
Câu hỏi: Định lý Pytago có thể được sử dụng để tính toán diện tích tam giác vuông không?
Trả lời: Không trực tiếp. Định lý Pytago dùng để tính độ dài cạnh. Tuy nhiên, khi biết độ dài các cạnh, ta có thể tính diện tích tam giác vuông bằng công thức 1/2 a b, với a và b là độ dài hai cạnh góc vuông. -
Câu hỏi: Có những cách chứng minh định lý Pytago nào khác?
Trả lời: Có rất nhiều cách chứng minh khác nhau, bao gồm chứng minh bằng hình học, đại số, và cả bằng phương pháp gấp giấy. -
Câu hỏi: Định lý Pytago có liên quan gì đến các công thức toán học khác?
Trả lời: Định lý Pytago là nền tảng cho nhiều công thức toán học khác, đặc biệt là trong hình học và lượng giác. Ví dụ, nó được sử dụng để suy ra công thức tính khoảng cách giữa hai điểm trong hệ tọa độ Descartes. -
Câu hỏi: Làm sao để nhớ công thức Pytago một cách dễ dàng?
Trả lời: Có nhiều cách để nhớ công thức này, ví dụ như sử dụng câu nói “bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. -
Câu hỏi: Tôi có thể tìm hiểu thêm về định lý Pytago ở đâu?
Trả lời: Bạn có thể tìm thấy nhiều thông tin về định lý Pytago trên internet, trong sách giáo khoa toán học, hoặc tại các thư viện. -
Câu hỏi: Ai là người đầu tiên phát hiện ra định lý Pytago?
Trả lời: Mặc dù định lý này được đặt theo tên Pythagoras, nhưng nó đã được biết đến từ trước đó ở các nền văn minh khác như Babylon và Ai Cập. Pythagoras được cho là người đầu tiên chứng minh định lý này một cách toán học. -
Câu hỏi: Định lý Pytago có ứng dụng trong đời sống hàng ngày không?
Trả lời: Có, định lý Pytago có rất nhiều ứng dụng trong đời sống hàng ngày, ví dụ như trong xây dựng, định vị, và thiết kế. công thức phi hàm euler cũng là một ví dụ về ứng dụng của toán học trong thực tế. -
Câu hỏi: Làm thế nào để áp dụng định lý Pytago vào bài toán cụ thể?
Trả lời: Đầu tiên, bạn cần xác định tam giác vuông trong bài toán. Sau đó, xác định cạnh huyền và hai cạnh góc vuông. Cuối cùng, áp dụng công thức a² + b² = c² để tính toán.
