Công Thức Cộng Xác Suất là một công cụ quan trọng trong việc phân tích và dự đoán các sự kiện, từ việc dự đoán kết quả tung xúc xắc đến việc đánh giá rủi ro trong kinh doanh. Bài viết này sẽ hướng dẫn bạn cách áp dụng công thức cộng xác suất một cách hiệu quả và chính xác.
Hiểu Rõ Về Công Thức Cộng Xác Suất
Công thức cộng xác suất cho phép chúng ta tính xác suất của ít nhất một trong số các sự kiện xảy ra. Nắm vững công thức này sẽ giúp bạn đưa ra quyết định sáng suốt hơn trong nhiều tình huống. Ví dụ, khi bạn muốn biết xác suất trúng ít nhất một giải trong một kỳ xổ số, công thức cộng xác suất sẽ giúp bạn tìm ra câu trả lời.
Các Loại Công Thức Cộng Xác Suất
Có hai dạng chính của công thức cộng xác suất: cho các sự kiện xung khắc và cho các sự kiện không xung khắc.
Công Thức Cho Sự Kiện Xung Khắc
Đối với các sự kiện xung khắc (tức là không thể xảy ra đồng thời), công thức cộng xác suất rất đơn giản: P(A hoặc B) = P(A) + P(B). Ví dụ, nếu bạn tung một con xúc xắc, sự kiện xuất hiện mặt 1 và sự kiện xuất hiện mặt 2 là xung khắc.
Công Thức Cho Sự Kiện Không Xung Khắc
Đối với các sự kiện không xung khắc (tức là có thể xảy ra đồng thời), công thức cộng xác suất phức tạp hơn một chút: P(A hoặc B) = P(A) + P(B) – P(A và B). P(A và B) là xác suất cả hai sự kiện A và B cùng xảy ra. Ví dụ, trong một bộ bài, việc rút được một lá bài vừa là Át vừa là Cơ là hai sự kiện không xung khắc.
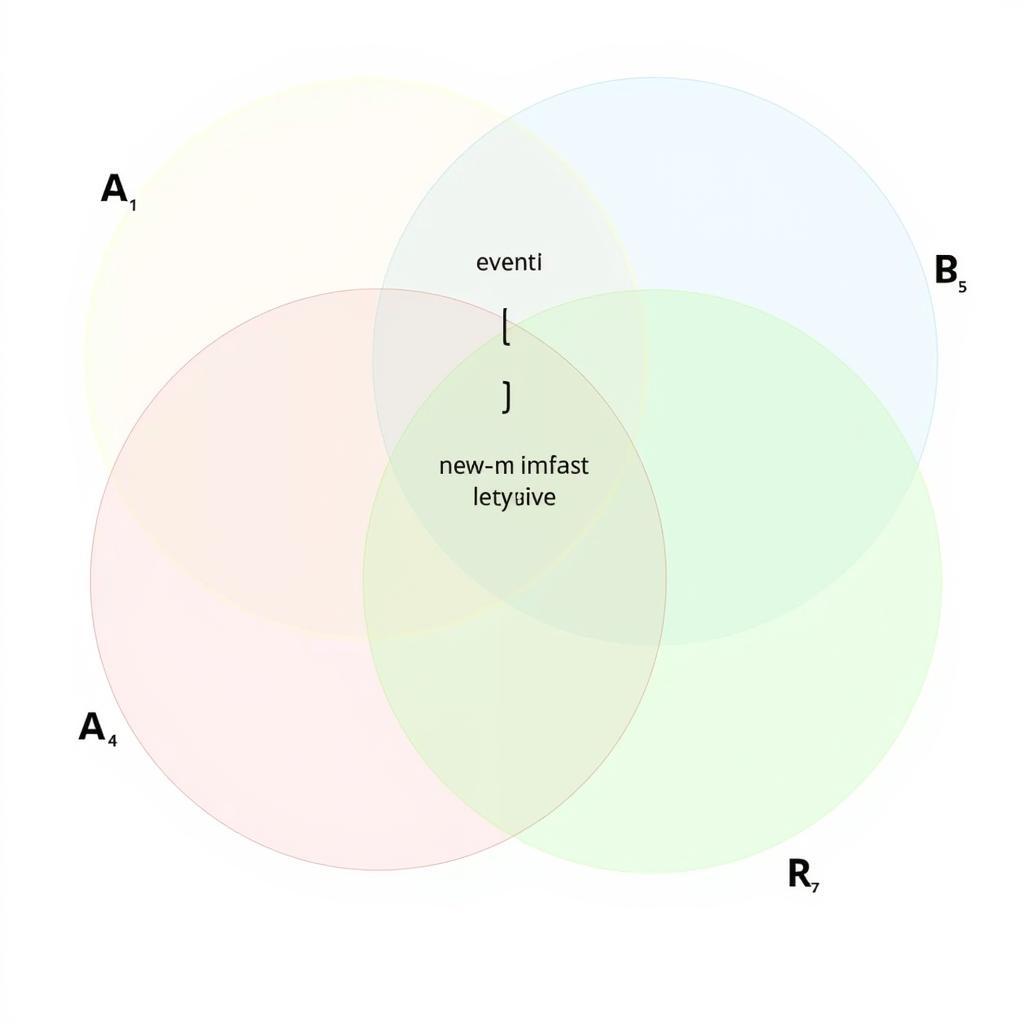 Công Thức Cộng Xác Suất Sự Kiện Không Xung Khắc
Công Thức Cộng Xác Suất Sự Kiện Không Xung Khắc
Ứng Dụng Của Công Thức Cộng Xác Suất
Công thức cộng xác suất có nhiều ứng dụng trong cuộc sống, từ việc tính toán xác suất trúng số đến việc đánh giá rủi ro trong đầu tư. Hiểu rõ cách áp dụng công thức này sẽ giúp bạn đưa ra những quyết định đúng đắn hơn.
Trong Đời Sống Hàng Ngày
Bạn có thể sử dụng công thức cộng xác suất để tính toán xác suất gặp mưa khi dự báo thời tiết cho biết có 30% khả năng mưa vào buổi sáng và 40% khả năng mưa vào buổi chiều.
Trong Khoa Học Và Kỹ Thuật
Công thức cộng xác suất được sử dụng rộng rãi trong các lĩnh vực như thống kê, khoa học máy tính và kỹ thuật. Ví dụ: các công thức trong sinh học cũng sử dụng nguyên lý xác suất.
What Công Thức Cộng Xác Suất?
Công thức cộng xác suất là một công thức toán học dùng để tính xác suất của ít nhất một trong số các sự kiện xảy ra.
Who Sử Dụng Công Thức Cộng Xác Suất?
Bất kỳ ai cũng có thể sử dụng công thức cộng xác suất, từ học sinh, sinh viên đến các chuyên gia trong lĩnh vực thống kê, khoa học dữ liệu và tài chính.
When Nên Sử Dụng Công Thức Cộng Xác Suất?
Bạn nên sử dụng công thức cộng xác suất khi cần tính xác suất của ít nhất một trong số các sự kiện xảy ra.
Where Ứng Dụng Công Thức Cộng Xác Suất?
Công thức cộng xác suất được ứng dụng trong nhiều lĩnh vực, từ đời sống hàng ngày đến khoa học và kỹ thuật.
Why Cần Học Công Thức Cộng Xác Suất?
Học công thức cộng xác suất giúp bạn hiểu rõ hơn về xác suất và đưa ra quyết định tốt hơn trong cuộc sống.
How Sử Dụng Công Thức Cộng Xác Suất?
Xác định các sự kiện và xác suất của chúng, sau đó áp dụng công thức cộng xác suất phù hợp. Đôi khi bạn cần phải tính toán những chỉ số khác như công thức tính dscr.
Nguyễn Văn A, chuyên gia thống kê, chia sẻ: “Công thức cộng xác suất là một công cụ vô cùng hữu ích giúp chúng ta hiểu và dự đoán các sự kiện ngẫu nhiên.”
Kết Luận
Công thức cộng xác suất là một công cụ quan trọng trong việc phân tích xác suất. Hiểu rõ và áp dụng đúng công thức này sẽ giúp bạn đưa ra những quyết định sáng suốt hơn. Ví dụ, bạn có thể sử dụng xác suất để phân tích công thức tính tổn thất điện áp.
FAQ
-
Câu hỏi 1: Sự khác biệt giữa sự kiện xung khắc và sự kiện không xung khắc là gì?
- Trả lời: Sự kiện xung khắc là hai sự kiện không thể xảy ra đồng thời. Sự kiện không xung khắc là hai sự kiện có thể xảy ra đồng thời.
-
Câu hỏi 2: Khi nào sử dụng công thức P(A hoặc B) = P(A) + P(B)?
- Trả lời: Khi A và B là hai sự kiện xung khắc.
-
Câu hỏi 3: Khi nào sử dụng công thức P(A hoặc B) = P(A) + P(B) – P(A và B)?
- Trả lời: Khi A và B là hai sự kiện không xung khắc.
-
Câu hỏi 4: Làm thế nào để tính P(A và B)?
- Trả lời: P(A và B) được tính dựa trên mối quan hệ giữa A và B. Nếu A và B là độc lập, P(A và B) = P(A) * P(B).
-
Câu hỏi 5: Công thức cộng xác suất có liên quan gì đến công thức tính gama đẩy nổi?
- Trả lời: Không liên quan trực tiếp. Công thức cộng xác suất liên quan đến xác suất, trong khi công thức tính gama đẩy nổi liên quan đến vật lý.
-
Câu hỏi 6: Có tài liệu nào để học thêm về công thức cộng xác suất không?
- Trả lời: Có rất nhiều tài liệu trực tuyến và sách giáo khoa về xác suất và thống kê.
-
Câu hỏi 7: Công thức cộng xác suất có thể áp dụng trong trò chơi may rủi không?
- Trả lời: Có, công thức cộng xác suất có thể được sử dụng để phân tích xác suất trong các trò chơi may rủi.
-
Câu hỏi 8: Công thức strings có liên quan gì đến công thức cộng xác suất không?
- Trả lời: Không liên quan. Công thức strings liên quan đến xử lý chuỗi ký tự trong lập trình.
-
Câu hỏi 9: Tôi có thể tìm hiểu thêm về xác suất ở đâu?
- Trả lời: Bạn có thể tìm hiểu thêm về xác suất qua sách giáo khoa, các khóa học trực tuyến, và các nguồn tài liệu khác trên internet.
-
Câu hỏi 10: Làm sao để áp dụng công thức cộng xác suất vào thực tế?
- Trả lời: Bằng cách xác định rõ các sự kiện và xác suất tương ứng, sau đó áp dụng công thức phù hợp với tình huống.
