Công Thức đạo Hàm Phân Số là một công cụ quan trọng trong giải tích, giúp chúng ta tìm tốc độ thay đổi của một hàm số được biểu diễn dưới dạng phân số. Việc nắm vững công thức này không chỉ giúp bạn giải quyết các bài toán trong học tập mà còn ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau.
Khám Phá Công Thức Đạo Hàm Phân Số
Đạo hàm của một phân số, hay nói cách khác là đạo hàm của thương của hai hàm số, được tính theo công thức sau:
Nếu u(x) và v(x) là hai hàm số khả vi và v(x) ≠ 0, thì đạo hàm của hàm số f(x) = u(x)/v(x) được tính theo công thức:
f'(x) = [u'(x)v(x) – u(x)v'(x)] / [v(x)]²
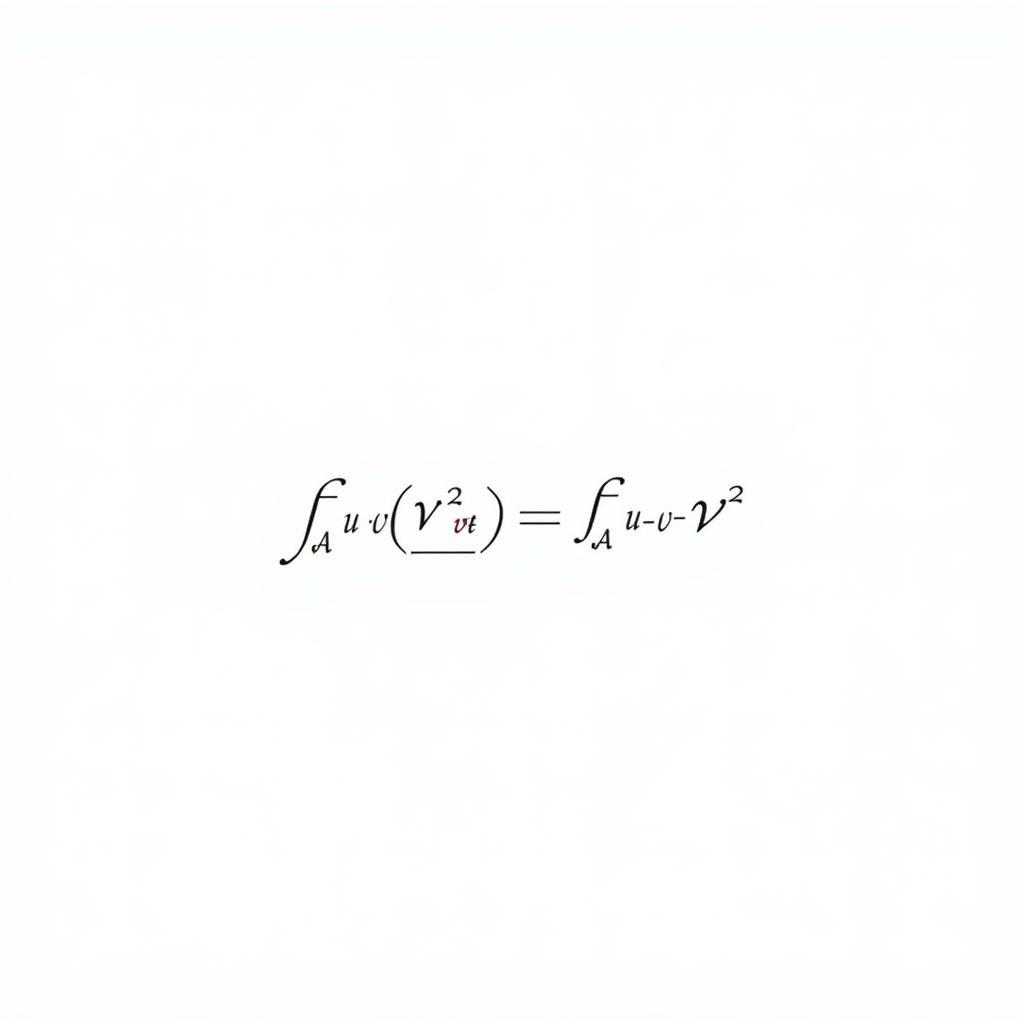 Công Thức Đạo Hàm Phân Số
Công Thức Đạo Hàm Phân Số
Nói một cách dễ hiểu hơn, đạo hàm của một phân số bằng “đạo hàm tử nhân mẫu trừ tử nhân đạo hàm mẫu, tất cả chia cho mẫu bình phương”. Công thức này có thể được chứng minh bằng cách sử dụng định nghĩa đạo hàm và quy tắc đạo hàm của tích.
Áp Dụng Công Thức Đạo Hàm Phân Số Qua Ví Dụ
Để hiểu rõ hơn về cách áp dụng công thức này, chúng ta hãy cùng xem xét một số ví dụ cụ thể.
- Ví dụ 1: Tính đạo hàm của hàm số f(x) = (x² + 1) / (2x – 3).
Ở đây, u(x) = x² + 1 và v(x) = 2x – 3. Ta có u'(x) = 2x và v'(x) = 2. Áp dụng công thức đạo hàm phân số, ta được:
f'(x) = [(2x)(2x – 3) – (x² + 1)(2)] / (2x – 3)² = (4x² – 6x – 2x² – 2) / (2x – 3)² = (2x² – 6x – 2) / (2x – 3)²
- Ví dụ 2: Tính đạo hàm của hàm số f(x) = sin(x) / cos(x) (tức là tan(x)).
Trong trường hợp này, u(x) = sin(x) và v(x) = cos(x). Ta có u'(x) = cos(x) và v'(x) = -sin(x). Áp dụng công thức, ta được:
f'(x) = [cos(x)cos(x) – sin(x)(-sin(x))] / cos²(x) = (cos²(x) + sin²(x)) / cos²(x) = 1 / cos²(x) = sec²(x)
Trả Lời Các Câu Hỏi
-
What công thức đạo hàm phân số? Công thức đạo hàm phân số là f'(x) = [u'(x)v(x) – u(x)v'(x)] / [v(x)]².
-
Who sử dụng công thức đạo hàm phân số? Học sinh, sinh viên, kỹ sư, nhà khoa học, và bất kỳ ai làm việc với giải tích đều sử dụng công thức này.
-
When nên sử dụng công thức đạo hàm phân số? Khi bạn cần tìm đạo hàm của một hàm số được biểu diễn dưới dạng phân số.
-
Where áp dụng công thức đạo hàm phân số? Công thức này được áp dụng trong nhiều lĩnh vực, từ toán học và vật lý đến kinh tế và kỹ thuật. Có lẽ bạn sẽ thích thú với công thức nước ép rau.
-
Why công thức đạo hàm phân số quan trọng? Nó giúp chúng ta hiểu tốc độ thay đổi của các hàm phân số, một khái niệm cơ bản trong giải tích.
-
How sử dụng công thức đạo hàm phân số? Xác định tử số và mẫu số, tính đạo hàm của từng hàm, sau đó áp dụng công thức. Tham khảo thêm công thức tính tốc độ phản ứng.
Bảng Giá Chi Tiết (Không áp dụng cho nội dung này)
Trích Dẫn Chuyên Gia
TS. Nguyễn Văn A, chuyên gia toán học, chia sẻ: “Công thức đạo hàm phân số là một trong những công thức quan trọng nhất trong giải tích. Nắm vững công thức này sẽ giúp bạn giải quyết được rất nhiều bài toán phức tạp.”
PGS. Trần Thị B, giảng viên đại học, cho biết: “Việc hiểu rõ cách áp dụng công thức đạo hàm phân số không chỉ giúp sinh viên đạt điểm cao trong các kỳ thi mà còn giúp họ phát triển tư duy logic và khả năng giải quyết vấn đề.” Bạn có thể tìm hiểu thêm về glucozo công thức cấu tạo.
Kết Luận
Công thức đạo hàm phân số là một công cụ mạnh mẽ trong giải tích, giúp chúng ta hiểu và tính toán tốc độ thay đổi của các hàm phân số. Việc nắm vững công thức này và luyện tập thường xuyên sẽ giúp bạn thành thạo trong việc giải quyết các bài toán liên quan đến đạo hàm. Có thể bạn cũng quan tâm đến các công thức smoothie giảm cân.
FAQ
-
Nêu công thức đạo hàm phân số?
- Đạo hàm của u/v là (u’v – uv’)/v².
-
Làm thế nào để nhớ công thức đạo hàm phân số?
- “Đạo hàm tử nhân mẫu trừ tử nhân đạo hàm mẫu, tất cả chia cho mẫu bình phương”.
-
Điều gì xảy ra nếu mẫu số bằng 0?
- Hàm số không xác định tại điểm đó, và đạo hàm cũng không tồn tại.
-
Có công cụ nào giúp tính đạo hàm phân số tự động không?
- Có, nhiều phần mềm toán học và trang web trực tuyến có thể tính đạo hàm tự động.
-
Tại sao cần học đạo hàm phân số?
- Nó là nền tảng cho nhiều khái niệm quan trọng khác trong giải tích và các lĩnh vực ứng dụng. Bạn có thể tham khảo công thức tính lũy tiến trong excel.
