Công Thức đường Cao Tam Giác Cân là một công cụ hữu ích giúp đơn giản hóa việc giải quyết các bài toán hình học liên quan. Nắm vững công thức này, bạn sẽ dễ dàng tính toán độ dài đường cao, diện tích, và các yếu tố khác của tam giác cân. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về công thức đường cao tam giác cân, từ cơ bản đến nâng cao, cùng với những ví dụ thực tế và lời khuyên hữu ích. bảng công thức sin cos
Đường Cao Tam Giác Cân là gì?
Đường cao của một tam giác cân là đoạn thẳng vuông góc kẻ từ đỉnh xuống cạnh đáy. Trong tam giác cân, đường cao cũng đồng thời là đường trung tuyến, đường phân giác, và đường trung trực của cạnh đáy. Đặc biệt, trong tam giác đều, ba đường cao bằng nhau và giao nhau tại một điểm.
Công Thức Tính Đường Cao Tam Giác Cân
Công thức tính đường cao (h) của tam giác cân được tính như sau:
h = √(a² - (b/2)²)
Trong đó:
hlà đường cao của tam giác cânalà độ dài cạnh bênblà độ dài cạnh đáy
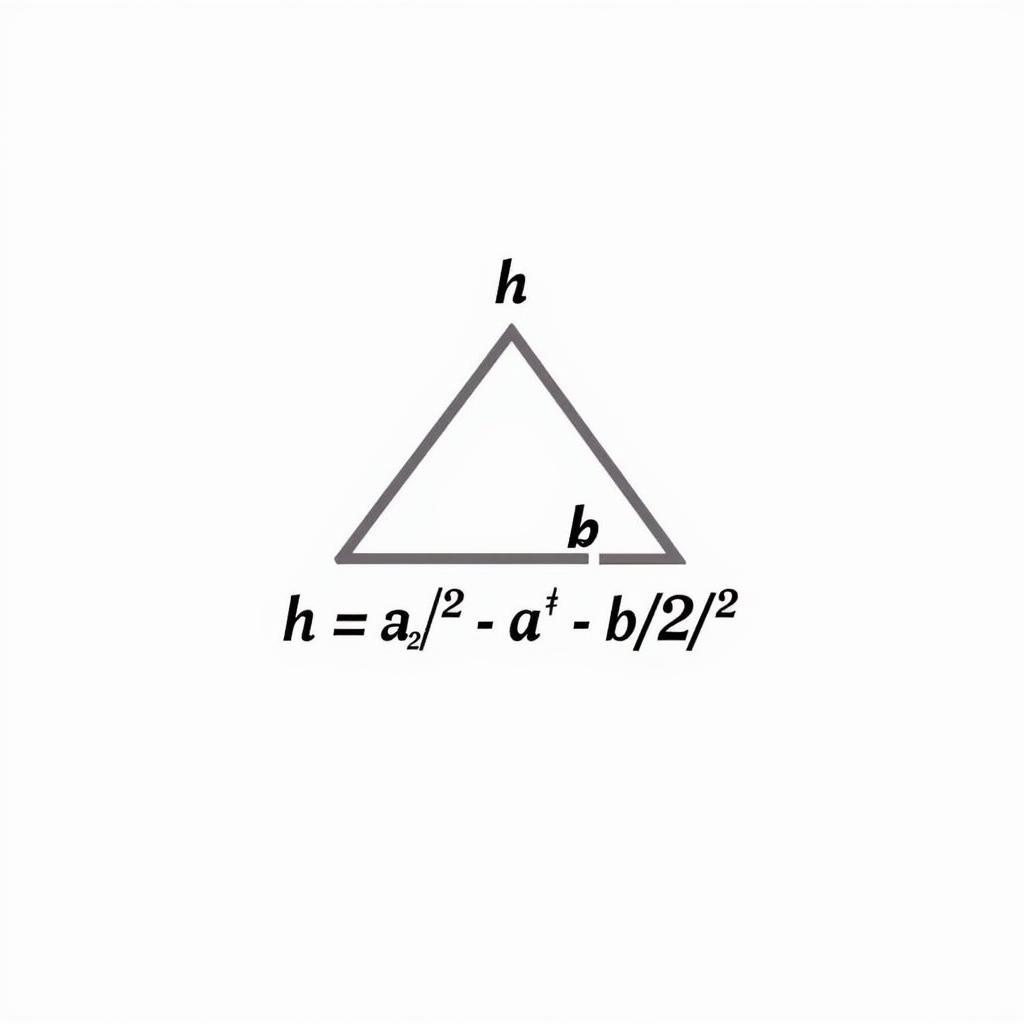Công Thức Đường Cao Tam Giác Cân
Ứng Dụng Công Thức Đường Cao Tam Giác Cân
Công thức đường cao tam giác cân có nhiều ứng dụng trong giải toán hình học. Ví dụ, bạn có thể sử dụng công thức này để tính diện tích tam giác cân, xác định tâm đường tròn ngoại tiếp, hay giải quyết các bài toán liên quan đến góc và cạnh của tam giác.
Tính Diện tích Tam Giác Cân
Diện tích (S) của tam giác cân được tính bằng công thức:
S = (1/2) * b * h
Xác Định Tâm Đường Tròn Ngoại Tiếp
Đường cao của tam giác cân giao nhau tại tâm đường tròn ngoại tiếp tam giác.
Ví Dụ Minh Họa
Cho tam giác cân ABC với cạnh bên AB = AC = 5cm và cạnh đáy BC = 6cm. Tính đường cao AH.
Áp dụng công thức: h = √(a² - (b/2)²)
Ta có: h = √(5² - (6/2)²) = √(25 - 9) = √16 = 4cm
Vậy đường cao AH của tam giác ABC là 4cm.
What công thức đường cao tam giác cân?
Công thức đường cao tam giác cân là h = √(a² - (b/2)²) với a là cạnh bên, b là cạnh đáy, và h là đường cao.
Who sử dụng công thức đường cao tam giác cân?
Học sinh, giáo viên, kỹ sư, và bất kỳ ai làm việc với hình học đều sử dụng công thức này.
When sử dụng công thức đường cao tam giác cân?
Công thức này được sử dụng khi cần tính toán đường cao, diện tích, hoặc các yếu tố khác của tam giác cân.
Where tìm thấy công thức đường cao tam giác cân?
Bạn có thể tìm thấy công thức này trong sách giáo khoa toán học, website giáo dục, và bài viết này. công thức tính sin
Why cần học công thức đường cao tam giác cân?
Hiểu công thức này giúp giải quyết các bài toán hình học liên quan đến tam giác cân một cách hiệu quả.
How áp dụng công thức đường cao tam giác cân?
Đơn giản chỉ cần thay các giá trị đã biết của cạnh bên và cạnh đáy vào công thức để tính đường cao.
“Việc nắm vững công thức đường cao tam giác cân là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn.” – Nguyễn Văn A, Giáo sư Toán học
“Công thức này không chỉ hữu ích trong học tập mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau.” – Trần Thị B, Kỹ sư xây dựng
Kết luận
Công thức đường cao tam giác cân là một công cụ quan trọng trong hình học. Nắm vững công thức này sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác. bài tập toán lớp 11 bài công thức niu tơn Hy vọng bài viết này đã cung cấp cho bạn kiến thức hữu ích về công thức đường cao tam giác cân. công thức tính đoạn thẳng các công thức tính hình học không gian lớp 12
FAQ
1. Đường cao tam giác cân có phải là đường trung tuyến không?
- Đúng vậy, trong tam giác cân, đường cao kẻ từ đỉnh xuống cạnh đáy cũng đồng thời là đường trung tuyến.
2. Làm thế nào để chứng minh công thức đường cao tam giác cân?
- Bạn có thể chứng minh công thức này bằng cách sử dụng định lý Pythagore trong tam giác vuông tạo bởi đường cao, một cạnh bên, và một nửa cạnh đáy.
3. Công thức đường cao tam giác cân có áp dụng được cho tam giác đều không?
- Có, tam giác đều là một trường hợp đặc biệt của tam giác cân, nên công thức vẫn áp dụng được.
4. Ngoài công thức này, còn cách nào khác để tính đường cao tam giác cân không?
- Có, bạn có thể sử dụng lượng giác hoặc các định lý hình học khác để tính đường cao.
5. Ứng dụng của công thức đường cao tam giác cân trong đời sống là gì?
- Công thức này được ứng dụng trong nhiều lĩnh vực như xây dựng, kiến trúc, thiết kế, và đo đạc.
6. Làm sao để nhớ công thức đường cao tam giác cân dễ dàng?
- Hãy luyện tập giải nhiều bài tập và liên hệ công thức với hình vẽ để ghi nhớ tốt hơn.
7. Nếu biết đường cao và cạnh đáy, làm thế nào để tính cạnh bên của tam giác cân?
- Bạn có thể sử dụng định lý Pythagore để tính cạnh bên.
8. Diện tích tam giác cân được tính như thế nào?
- Diện tích tam giác cân bằng một nửa tích của cạnh đáy và đường cao.
9. Đường cao tam giác cân có tính chất gì đặc biệt?
- Trong tam giác cân, đường cao vừa là đường trung tuyến, đường phân giác, và đường trung trực của cạnh đáy.
10. Tìm hiểu thêm về công thức đường cao tam giác cân ở đâu?
- Bạn có thể tìm thấy nhiều tài liệu về chủ đề này trên internet, sách giáo khoa toán học, và các nguồn học tập khác.