Công Thức Lượng Tam Giác Vuông là nền tảng quan trọng trong toán học, đặc biệt là hình học. Nắm vững các công thức này không chỉ giúp bạn giải quyết các bài toán liên quan đến tam giác vuông mà còn mở ra cánh cửa chinh phục những kiến thức toán học phức tạp hơn. công thức lượng giác tam giác vuông
Định Nghĩa và Các Công Thức Cơ Bản
Trong tam giác vuông, ngoài định lý Pytago quen thuộc, chúng ta còn có hệ thống các công thức lượng giác. Các công thức này liên hệ giữa các cạnh và các góc của tam giác vuông, tạo nên một mạng lưới kiến thức chặt chẽ.
- Công thức sin: sin(α) = cạnh đối / cạnh huyền
- Công thức cos: cos(α) = cạnh kề / cạnh huyền
- Công thức tan: tan(α) = cạnh đối / cạnh kề
- Công thức cot: cot(α) = cạnh kề / cạnh đối
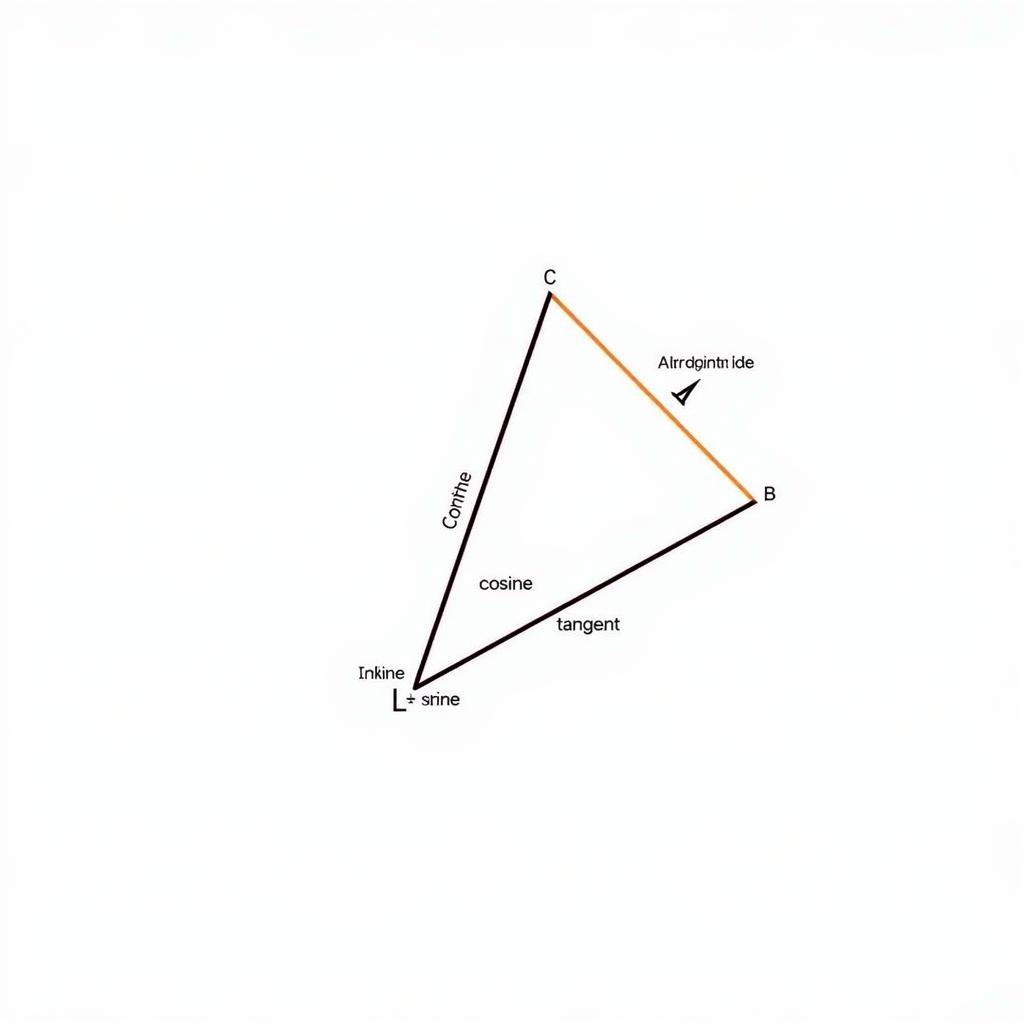Công thức lượng giác tam giác vuông cơ bản
Mối Liên Hệ Giữa Các Công Thức Lượng Giác
Các công thức lượng giác không tồn tại độc lập mà có mối liên hệ chặt chẽ với nhau. Ví dụ, ta có:
- tan(α) = sin(α) / cos(α)
- cot(α) = 1 / tan(α)
- sin²(α) + cos²(α) = 1
Hiểu rõ mối quan hệ này giúp bạn linh hoạt biến đổi và áp dụng các công thức trong giải toán.
Ứng Dụng Công Thức Lượng Tam Giác Vuông trong Thực Tế
Công thức lượng tam giác vuông không chỉ nằm trên trang sách mà còn có ứng dụng rộng rãi trong thực tế. Từ việc đo đạc chiều cao của tòa nhà đến tính toán khoảng cách trong thiên văn học, các công thức này đóng vai trò then chốt.
Ứng dụng công thức lượng giác trong thực tế
Trả Lời Các Câu Hỏi
- What công thức lượng tam giác vuông? Công thức lượng tam giác vuông là tập hợp các công thức liên hệ giữa các cạnh và góc trong tam giác vuông.
- Who sử dụng công thức lượng tam giác vuông? Học sinh, sinh viên, kỹ sư, kiến trúc sư, và nhiều ngành nghề khác đều sử dụng công thức này.
- When cần dùng công thức lượng tam giác vuông? Khi cần tính toán các đại lượng liên quan đến tam giác vuông, đặc biệt là trong hình học và các ứng dụng thực tế.
- Where áp dụng công thức lượng tam giác vuông? Trong toán học, vật lý, thiên văn học, kiến trúc, xây dựng, và nhiều lĩnh vực khác.
- Why công thức lượng tam giác vuông quan trọng? Chúng là nền tảng cho nhiều kiến thức toán học và ứng dụng thực tế.
- How sử dụng công thức lượng tam giác vuông? Xác định các đại lượng đã biết và áp dụng công thức phù hợp để tính toán đại lượng cần tìm.
Bảng Giá Chi Tiết (Không áp dụng)
Trích dẫn từ Chuyên gia
Ông Nguyễn Văn A, giáo sư toán học tại Đại học X, cho biết: “Công thức lượng tam giác vuông là kiến thức nền tảng không thể thiếu cho bất kỳ ai muốn học tốt toán hình.”
Bà Trần Thị B, kỹ sư xây dựng, chia sẻ: “Trong công việc của tôi, công thức lượng tam giác vuông được sử dụng hàng ngày để tính toán và thiết kế công trình.”
Ví dụ về công thức lượng giác tam giác vuông
Kết luận
Công thức lượng tam giác vuông là kiến thức cốt lõi trong toán học và có ứng dụng rộng rãi trong đời sống. Hiểu rõ và vận dụng thành thạo các công thức này sẽ giúp bạn giải quyết nhiều vấn đề toán học và thực tiễn một cách hiệu quả. Hãy tiếp tục nghiên cứu và khám phá thêm về toán lớp 10 công thức lượng giác để nâng cao kiến thức của mình.
FAQ
-
Nêu các công thức lượng giác trong tam giác vuông?
- sin(α) = đối/huyền, cos(α) = kề/huyền, tan(α) = đối/kề, cot(α) = kề/đối.
-
Định lý Pytago là gì?
- Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
-
Làm thế nào để nhớ các công thức lượng giác?
- Có nhiều cách, ví dụ như sử dụng câu thần chú “SOH CAH TOA”.
-
Các công thức tính góc trong oxyz có liên quan đến công thức lượng giác tam giác vuông không?
- Có, chúng có mối liên hệ nhất định, đặc biệt khi chiếu các vector lên mặt phẳng.
-
Công thức tính diện tích các hình lớp 5 có sử dụng công thức lượng giác không?
- Ở lớp 5, chưa sử dụng công thức lượng giác, nhưng sẽ là nền tảng cho việc học sau này.
-
Công thức tính lãi cộng dồn có liên quan gì đến công thức lượng giác không?
- Không, công thức tính lãi cộng dồn thuộc về lĩnh vực tài chính.
-
Làm thế nào để áp dụng công thức lượng giác vào bài toán thực tế?
- Xác định tam giác vuông, xác định các đại lượng đã biết và cần tìm, sau đó áp dụng công thức phù hợp.
-
Có tài liệu nào giúp tôi luyện tập thêm về công thức lượng giác không?
- Có rất nhiều sách giáo khoa, bài tập, và tài liệu trực tuyến.
-
Công thức lượng giác tam giác vuông có áp dụng cho tam giác thường không?
- Không trực tiếp, nhưng ta có thể chia tam giác thường thành các tam giác vuông để áp dụng.
-
Tại sao sin²α + cos²α = 1?
- Đây là một hệ thức cơ bản trong lượng giác, xuất phát từ định lý Pytago.