Công Thức Tích Vô Hướng 2 Vecto là một khái niệm quan trọng trong toán học, đặc biệt là trong hình học và đại số tuyến tính. Bài viết này sẽ đi sâu vào phân tích công thức này, từ định nghĩa cơ bản đến các ứng dụng thực tiễn, giúp bạn nắm vững kiến thức và vận dụng hiệu quả.
Định Nghĩa Tích Vô Hướng Của Hai Vecto
Tích vô hướng của hai vecto $vec{a}$ và $vec{b}$, ký hiệu là $vec{a} cdot vec{b}$, được định nghĩa bằng tích độ dài của hai vecto nhân với cosin của góc giữa chúng. Nói cách khác: $vec{a} cdot vec{b} = |vec{a}| cdot |vec{b}| cdot cos(vec{a}, vec{b})$.
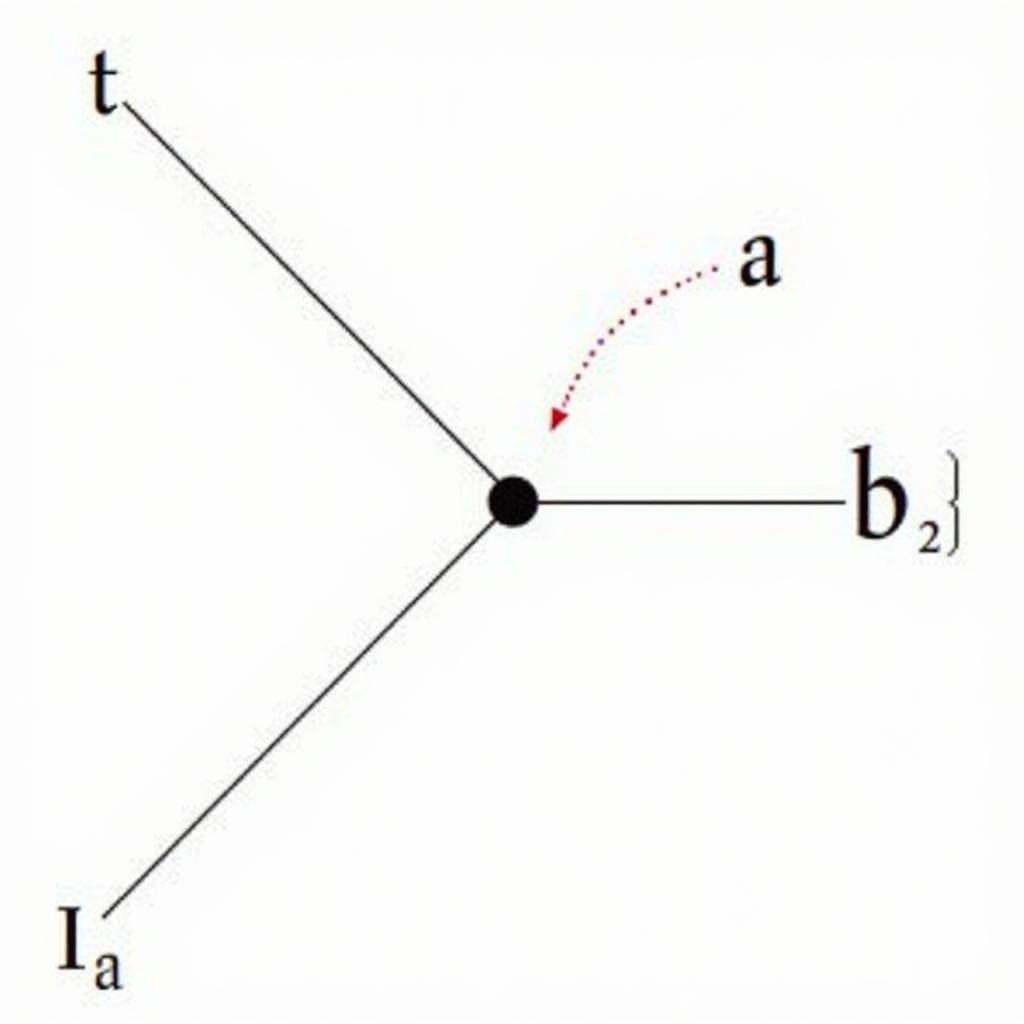Minh họa tích vô hướng hai vecto
Tích vô hướng cho ra một giá trị vô hướng, tức là một số thực, chứ không phải một vecto. Điều này khác biệt với tích có hướng, một phép toán khác giữa hai vecto cho ra một vecto mới. Việc hiểu rõ công thức tính độ dài vecto là nền tảng để nắm vững tích vô hướng.
Tính Chất Của Tích Vô Hướng
Tích vô hướng có một số tính chất quan trọng, bao gồm tính giao hoán, tính phân phối, và tính kết hợp với phép nhân vô hướng. Những tính chất này cho phép chúng ta biến đổi và tính toán tích vô hướng một cách linh hoạt.
Biểu Thức Tọa Độ Của Tích Vô Hướng
Trong hệ tọa độ Descartes, nếu $vec{a} = (a_1, a_2, a_3)$ và $vec{b} = (b_1, b_2, b_3)$, thì tích vô hướng của chúng được tính bằng: $vec{a} cdot vec{b} = a_1b_1 + a_2b_2 + a_3b_3$. Công thức này rất hữu ích trong việc tính toán thực tế. Đối với học sinh lớp 10, việc nắm vững công thức tích vô hướng lớp 10 là rất quan trọng.
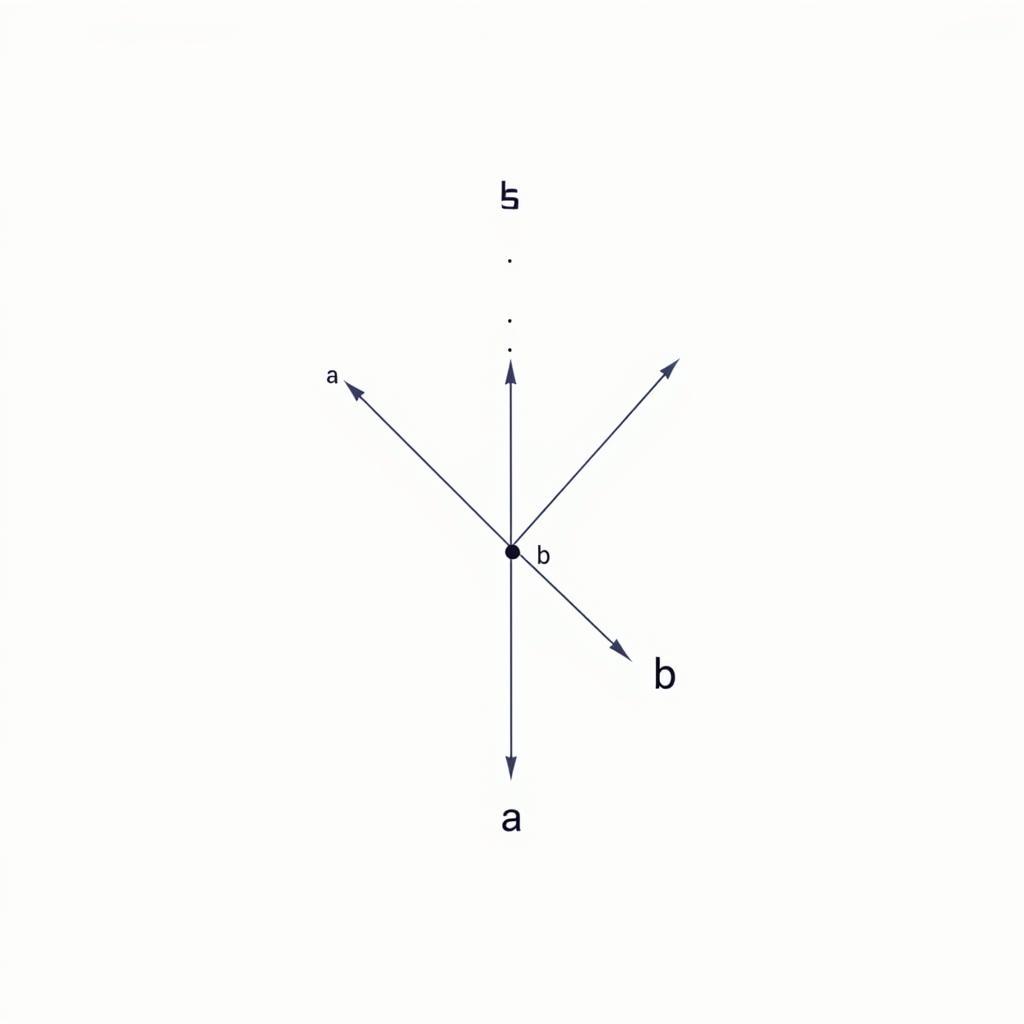Biểu diễn tọa độ của tích vô hướng
Ứng Dụng Của Tích Vô Hướng
Tích vô hướng có nhiều ứng dụng trong toán học và các lĩnh vực khác, chẳng hạn như vật lý và khoa học máy tính. Một số ứng dụng tiêu biểu bao gồm tính góc giữa hai vecto, tính chiều dài hình chiếu của một vecto lên một vecto khác, và kiểm tra xem hai vecto có vuông góc với nhau hay không. Kiến thức về tích vô hướng cũng rất quan trọng trong việc học bảng công thức toán hình học 12.
Trả Lời Các Câu Hỏi
- What công thức tích vô hướng 2 vecto? Công thức tích vô hướng 2 vecto là $vec{a} cdot vec{b} = |vec{a}| cdot |vec{b}| cdot cos(vec{a}, vec{b})$ hoặc $vec{a} cdot vec{b} = a_1b_1 + a_2b_2 + a_3b_3$ trong hệ tọa độ.
- Who sử dụng công thức tích vô hướng 2 vecto? Học sinh, sinh viên, kỹ sư, nhà khoa học, và lập trình viên đều sử dụng công thức này.
- When cần sử dụng công thức tích vô hướng 2 vecto? Khi cần tính toán liên quan đến góc, hình chiếu, hoặc kiểm tra tính vuông góc giữa hai vecto.
- Where áp dụng công thức tích vô hướng 2 vecto? Trong toán học, vật lý, khoa học máy tính, và nhiều lĩnh vực khác.
- Why công thức tích vô hướng 2 vecto quan trọng? Nó cung cấp một công cụ mạnh mẽ để phân tích và giải quyết các bài toán liên quan đến vecto.
- How tính toán công thức tích vô hướng 2 vecto? Nhân độ dài hai vecto với cosin góc giữa chúng, hoặc nhân các thành phần tương ứng rồi cộng lại.
Ứng dụng của tích vô hướng trong vật lý
Theo GS.TS Nguyễn Văn A, chuyên gia toán học hàng đầu: “Tích vô hướng là một công cụ không thể thiếu trong việc nghiên cứu các vấn đề về hình học và đại số tuyến tính.”
TS. Lê Thị B, nhà nghiên cứu vật lý lý thuyết: “Tích vô hướng đóng vai trò quan trọng trong việc mô tả các hiện tượng vật lý, ví dụ như công của một lực.”
Kết luận
Công thức tích vô hướng 2 vecto là một công cụ toán học quan trọng với nhiều ứng dụng rộng rãi. Hiểu rõ định nghĩa, tính chất, và cách tính toán công thức này sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan đến vecto. Việc áp dụng công thức tính giá bán hoặc công thức tính tổng các số lẻ cũng đòi hỏi sự chính xác tương tự như khi làm việc với tích vô hướng.
FAQ
-
Nêu Câu Hỏi: Tích vô hướng có hướng không?
Trả Lời Chi tiết Câu Hỏi: Không, tích vô hướng cho ra một giá trị vô hướng (một số thực), không phải một vecto. -
Nêu Câu Hỏi: Làm sao để phân biệt tích vô hướng và tích có hướng?
Trả Lời Chi tiết Câu Hỏi: Tích vô hướng cho ra một số, còn tích có hướng cho ra một vecto. -
Nêu Câu Hỏi: Tích vô hướng của hai vecto vuông góc bằng bao nhiêu?
Trả Lời Chi tiết Câu Hỏi: Bằng 0. -
Nêu Câu Hỏi: Tích vô hướng có thể âm không?
Trả Lời Chi tiết Câu Hỏi: Có, nếu góc giữa hai vecto lớn hơn 90 độ. -
Nêu Câu Hỏi: Ứng dụng của tích vô hướng trong đồ họa máy tính là gì?
Trả Lời Chi tiết Câu Hỏi: Được sử dụng để tính toán ánh sáng, bóng đổ, và xác định vị trí tương đối của các vật thể. -
Nêu Câu Hỏi: Tích vô hướng có liên quan gì đến độ dài của một vecto?
Trả Lời Chi tiết Câu Hỏi: Bình phương độ dài của một vecto bằng tích vô hướng của vecto đó với chính nó. -
Nêu Câu Hỏi: Có thể sử dụng tích vô hướng để tính diện tích hình bình hành không?
Trả Lời Chi tiết Câu Hỏi: Không trực tiếp, nhưng có thể sử dụng tích có hướng để tính diện tích hình bình hành. -
Nêu Câu Hỏi: Tích vô hướng có tính chất gì đặc biệt?
Trả Lời Chi tiết Câu Hỏi: Tính giao hoán, tính phân phối, và tính kết hợp với phép nhân vô hướng. -
Nêu Câu Hỏi: Làm thế nào để tính góc giữa hai vecto bằng tích vô hướng?
Trả Lời Chi tiết Câu Hỏi: Sử dụng công thức $cos(vec{a}, vec{b}) = frac{vec{a} cdot vec{b}}{|vec{a}| cdot |vec{b}|}$. -
Nêu Câu Hỏi: Tích vô hướng có ứng dụng gì trong học máy?
Trả Lời Chi tiết Câu Hỏi: Được sử dụng trong các thuật toán như Support Vector Machine (SVM) và phân tích thành phần chính (PCA).