Công Thức Tính Cạnh Góc Vuông Trong Tam Giác Vuông là kiến thức nền tảng trong hình học, giúp chúng ta giải quyết nhiều bài toán thực tế. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về công thức này, từ cơ bản đến nâng cao, kèm theo ví dụ minh họa và các câu hỏi thường gặp.
Định Lý Pythagoras và Công Thức Tính Cạnh Góc Vuông
Trong tam giác vuông, cạnh đối diện với góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông. Mối quan hệ giữa ba cạnh này được biểu diễn bằng Định lý Pythagoras: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Từ định lý này, ta có thể suy ra công thức tính cạnh góc vuông. Giả sử tam giác vuông ABC, với góc vuông tại A, cạnh huyền BC = a, hai cạnh góc vuông AB = c và AC = b. Ta có: a² = b² + c². Vậy, công thức tính cạnh góc vuông là: b = √(a² – c²) và c = √(a² – b²). Nắm vững công thức này sẽ giúp bạn dễ dàng tính toán độ dài các cạnh trong tam giác vuông. Bạn có thể tìm hiểu thêm về các công thức liên quan tại bảng công thức lượng giác.
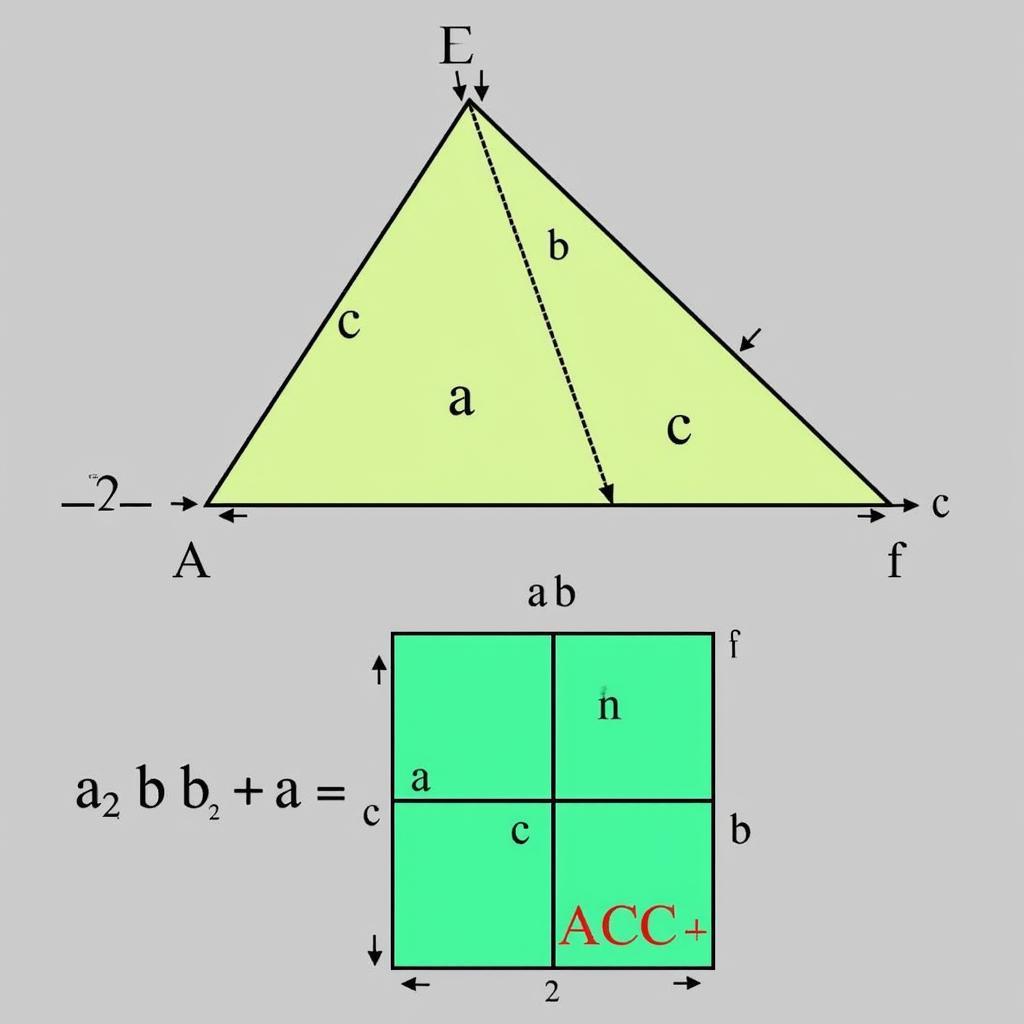 Công thức tính cạnh góc vuông trong tam giác vuông
Công thức tính cạnh góc vuông trong tam giác vuông
Ứng Dụng Công Thức Tính Cạnh Góc Vuông
Công thức tính cạnh góc vuông không chỉ giới hạn trong sách vở mà còn được ứng dụng rộng rãi trong thực tế. Ví dụ, trong xây dựng, để tính chiều dài của thanh giằng cho mái nhà, chúng ta cần áp dụng công thức này. Tương tự, trong đo đạc, xác định khoảng cách giữa hai điểm cũng sử dụng nguyên lý của tam giác vuông và công thức tính cạnh. Việc hiểu rõ các công thức tính diện tích tam giác cũng rất hữu ích trong nhiều trường hợp.
Ví Dụ Minh Họa
Cho tam giác vuông ABC, vuông tại A, biết cạnh huyền BC = 10cm và cạnh góc vuông AB = 6cm. Tính độ dài cạnh góc vuông AC.
Áp dụng công thức: AC = √(BC² – AB²) = √(10² – 6²) = √64 = 8cm.
Các Trường Hợp Đặc Biệt
Trong một số trường hợp đặc biệt, việc tính toán sẽ đơn giản hơn. Ví dụ, nếu tam giác vuông là tam giác vuông cân, hai cạnh góc vuông sẽ bằng nhau. Hoặc nếu biết một góc nhọn và một cạnh, ta có thể sử dụng tỉ số lượng giác để tính cạnh góc vuông.
Mẹo Ghi Nhớ Công Thức
Để dễ dàng ghi nhớ công thức, bạn có thể liên tưởng đến hình ảnh một hình vuông được chia thành hai hình vuông nhỏ hơn. Hình vuông lớn đại diện cho bình phương cạnh huyền, hai hình vuông nhỏ đại diện cho bình phương hai cạnh góc vuông.
What Công Thức Tính Cạnh Góc Vuông Trong Tam Giác Vuông?
Công thức dựa trên định lý Pythagoras: cạnh góc vuông = căn bậc hai của (cạnh huyền bình phương – cạnh góc vuông kia bình phương).
Who Sử Dụng Công Thức Này?
Học sinh, kỹ sư, kiến trúc sư, và bất kỳ ai làm việc với hình học và đo lường.
When Cần Áp Dụng Công Thức Này?
Khi cần tính toán độ dài cạnh góc vuông trong tam giác vuông, biết độ dài cạnh huyền và một cạnh góc vuông khác.
Where Tìm Thấy Công Thức Này?
Trong sách giáo khoa toán học, tài liệu kỹ thuật, và các trang web giáo dục trực tuyến.
Why Công Thức Này Quan Trọng?
Nó là nền tảng của hình học và được ứng dụng rộng rãi trong nhiều lĩnh vực.
How Sử Dụng Công Thức Này?
Xác định cạnh huyền và cạnh góc vuông đã biết, sau đó áp dụng công thức để tính cạnh góc vuông còn lại. Có thể bạn quan tâm đến công thức tứ giác đều.
“Hiểu rõ công thức tính cạnh góc vuông là chìa khóa để giải quyết nhiều bài toán hình học phức tạp,” – GS.TS Nguyễn Văn A, chuyên gia hình học.
 Ứng dụng thực tế của công thức tính cạnh góc vuông
Ứng dụng thực tế của công thức tính cạnh góc vuông
“Việc luyện tập thường xuyên sẽ giúp bạn thành thạo trong việc áp dụng công thức,” – ThS. Phạm Thị B, giảng viên toán học.
Kết luận
Công thức tính cạnh góc vuông trong tam giác vuông là một công cụ quan trọng trong hình học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và bài thơ về công thức tan giúp bạn ghi nhớ dễ dàng hơn.
FAQ
- Nêu công thức tính cạnh góc vuông? Cạnh góc vuông = căn bậc hai của (cạnh huyền bình phương – cạnh góc vuông kia bình phương).
- Định lý Pythagoras là gì? Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
- Làm thế nào để nhớ công thức tính cạnh góc vuông? Liên tưởng đến hình ảnh hình vuông lớn được chia thành hai hình vuông nhỏ.
- Ứng dụng của công thức này trong thực tế là gì? Xây dựng, đo đạc, thiết kế, v.v.
- Khi nào cần sử dụng công thức này? Khi biết cạnh huyền và một cạnh góc vuông, cần tính cạnh góc vuông còn lại.
- Có cách nào khác để tính cạnh góc vuông không? Có thể sử dụng tỉ số lượng giác nếu biết một góc nhọn và một cạnh.
- Tam giác vuông cân là gì? Tam giác vuông có hai cạnh góc vuông bằng nhau.
- Công thức tính cạnh góc vuông có liên quan gì đến diện tích tam giác? Cạnh góc vuông được sử dụng để tính diện tích tam giác vuông. Tìm hiểu thêm về diện tích lăng trụ công thức.
- Làm thế nào để thành thạo công thức này? Luyện tập thường xuyên với các bài toán khác nhau.
- Tài liệu nào cung cấp thông tin về công thức này? Sách giáo khoa toán, tài liệu kỹ thuật, và internet.
