Công Thức Tính Cạnh Huyền Góc Vuông là nền tảng quan trọng trong toán học, đặc biệt là hình học. Bài viết này sẽ giúp bạn nắm vững công thức này, từ cách áp dụng cơ bản đến những mẹo tính toán nhanh chóng và chính xác.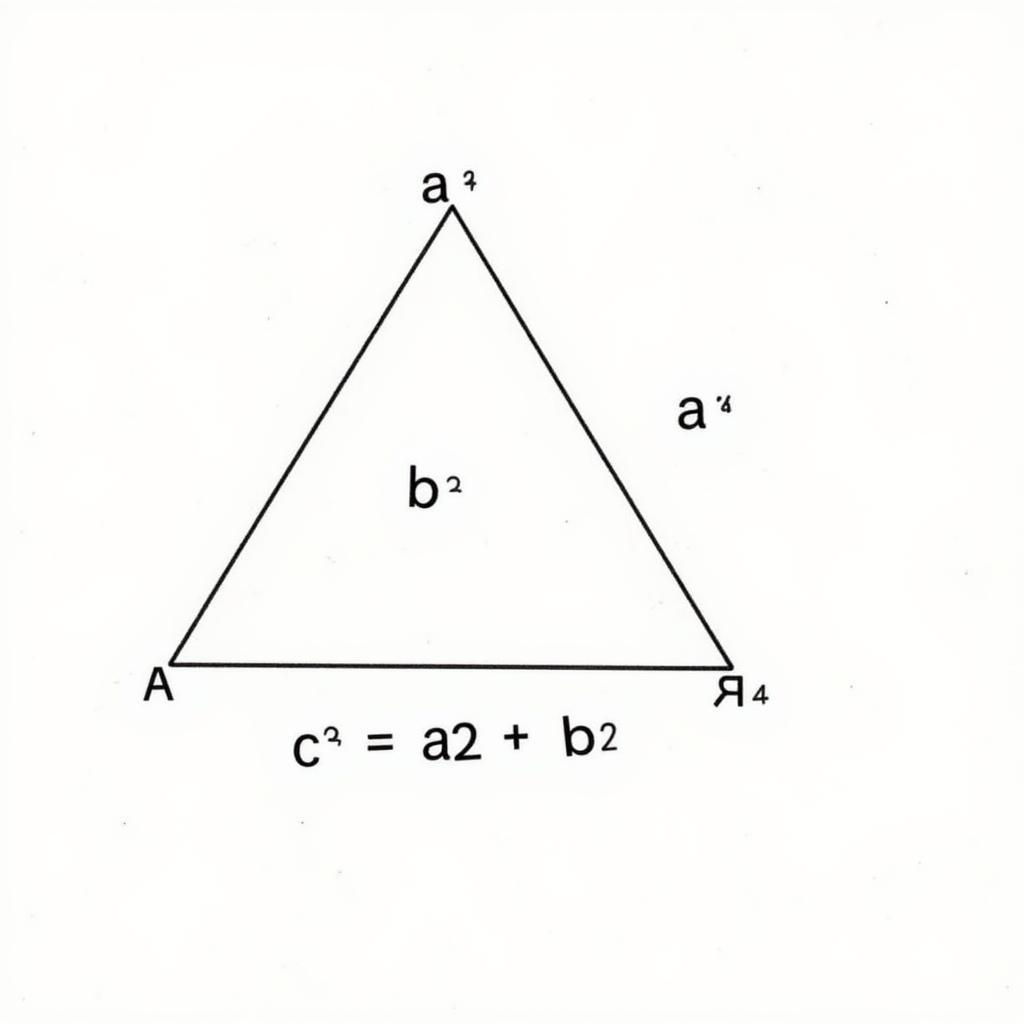 
Công thức tính cạnh huyền của tam giác vuông
Định Lý Pythagoras và Công Thức Tính Cạnh Huyền
Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền. Định lý Pythagoras chính là chìa khóa để tính toán độ dài cạnh huyền này. Định lý phát biểu rằng: “Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông”. Từ định lý này, ta có công thức tính cạnh huyền góc vuông như sau: c² = a² + b², trong đó:
- c là độ dài cạnh huyền
- a và b là độ dài hai cạnh góc vuông
Áp dụng công thức tính cạnh huyền
Ví dụ, nếu a = 3 và b = 4, thì c² = 3² + 4² = 9 + 16 = 25. Do đó, c = √25 = 5. công thức chu vi của tam giác cũng là một kiến thức quan trọng trong hình học.
Ứng Dụng Của Công Thức Tính Cạnh Huyền Góc Vuông trong Đời Sống
Công thức tính cạnh huyền không chỉ là kiến thức sách vở mà còn được ứng dụng rộng rãi trong thực tiễn. Từ việc đo đạc trong xây dựng, thiết kế kiến trúc, đến định vị GPS, công thức này đều đóng vai trò quan trọng.
Xây Dựng và Kiến Trúc
Trong xây dựng, công thức này giúp tính toán độ dài của dầm, cột, mái nhà, và nhiều cấu trúc khác. Kiến trúc sư cũng sử dụng công thức này để thiết kế các hình dạng và kích thước chính xác cho công trình.
Định vị GPS
Hệ thống định vị toàn cầu (GPS) sử dụng công thức tính cạnh huyền để xác định khoảng cách giữa các điểm trên trái đất. Việc tính toán này dựa trên tọa độ của các vệ tinh và thiết bị nhận tín hiệu GPS. Bạn có biết công thức sin có cũng được ứng dụng trong định vị không?
Mẹo Tính Nhanh Cạnh Huyền Với Một Số Trường Hợp Đặc Biệt
Đối với một số tam giác vuông đặc biệt, việc tính toán cạnh huyền có thể được thực hiện nhanh chóng hơn bằng cách ghi nhớ một số tỷ lệ đặc biệt.
Tam Giác Vuông Cân
Nếu tam giác vuông là tam giác vuông cân, nghĩa là hai cạnh góc vuông bằng nhau (a = b), thì công thức tính cạnh huyền trở thành c = a√2.
Tam Giác Vuông Có Góc 30-60-90
Trong tam giác vuông có các góc là 30, 60 và 90 độ, cạnh đối diện với góc 30 độ bằng một nửa cạnh huyền. 
Tam giác vuông đặc biệt
Trả Lời Các Câu Hỏi
- What công thức tính cạnh huyền góc vuông? Công thức là c² = a² + b², với c là cạnh huyền, a và b là hai cạnh góc vuông.
- Who sử dụng công thức tính cạnh huyền góc vuông? Kỹ sư, kiến trúc sư, nhà khoa học, và bất kỳ ai làm việc với hình học đều sử dụng công thức này.
- When nên sử dụng công thức tính cạnh huyền góc vuông? Khi bạn cần tìm độ dài cạnh huyền của một tam giác vuông.
- Where áp dụng công thức tính cạnh huyền góc vuông? Công thức này được áp dụng trong nhiều lĩnh vực, từ xây dựng, kiến trúc, đến định vị GPS.
- Why công thức tính cạnh huyền góc vuông quan trọng? Nó là nền tảng của hình học và có nhiều ứng dụng thực tiễn.
- How tính cạnh huyền góc vuông? Áp dụng công thức c² = a² + b² và tính căn bậc hai của kết quả.
Ông Nguyễn Văn A, một kỹ sư xây dựng giàu kinh nghiệm, chia sẻ: “Công thức tính cạnh huyền là công cụ không thể thiếu trong công việc của tôi. Nó giúp tôi tính toán chính xác kích thước của các cấu trúc, đảm bảo sự an toàn và ổn định cho công trình.” tổng hợp công thức toán hình 9 cung cấp kiến thức tổng quan về hình học lớp 9.
Bà Trần Thị B, một giáo viên toán học, cho biết: “Việc hiểu rõ công thức tính cạnh huyền là bước đầu tiên để học tốt hình học. Học sinh cần nắm vững công thức này và biết cách áp dụng nó vào các bài toán thực tế.” Có thể bạn cũng quan tâm đến công thức euler hình học.
Kết luận
Công thức tính cạnh huyền góc vuông là một công cụ toán học quan trọng với nhiều ứng dụng thực tiễn. Hy vọng bài viết này đã giúp bạn hiểu rõ về công thức này và cách áp dụng nó. Hãy luyện tập thường xuyên để thành thạo việc tính toán cạnh huyền và chinh phục mọi bài toán hình học. công thức hóa học của đường nho là một chủ đề thú vị khác bạn có thể tìm hiểu.
FAQ
-
Câu hỏi: Định lý Pythagoras là gì?
Trả lời: Định lý Pythagoras phát biểu rằng trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. -
Câu hỏi: Làm thế nào để tính cạnh huyền của tam giác vuông cân?
Trả lời: Cạnh huyền của tam giác vuông cân bằng cạnh góc vuông nhân với căn bậc hai của 2. -
Câu hỏi: Ứng dụng của công thức tính cạnh huyền trong đời sống là gì?
Trả lời: Công thức này được ứng dụng trong xây dựng, kiến trúc, định vị GPS, và nhiều lĩnh vực khác. -
Câu hỏi: Làm sao để nhớ công thức tính cạnh huyền?
Trả lời: Hãy liên tưởng đến hình ảnh tam giác vuông và ghi nhớ câu “bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. -
Câu hỏi: Có những mẹo nào để tính nhanh cạnh huyền không?
Trả lời: Đối với tam giác vuông cân và tam giác vuông 30-60-90, có những tỷ lệ đặc biệt giúp tính nhanh cạnh huyền. -
Câu hỏi: Tôi có thể tìm thêm tài liệu về công thức tính cạnh huyền ở đâu?
Trả lời: Bạn có thể tìm thấy nhiều tài liệu trực tuyến, sách giáo khoa toán học, và các video hướng dẫn. -
Câu hỏi: Công thức tính cạnh huyền có liên quan đến các công thức toán học nào khác?
Trả lời: Công thức này liên quan đến các công thức tính diện tích, chu vi tam giác, cũng như các định lý hình học khác. -
Câu hỏi: Tại sao cần phải học công thức tính cạnh huyền?
Trả lời: Nó là kiến thức cơ bản trong toán học và có nhiều ứng dụng trong thực tế. -
Câu hỏi: Có phần mềm nào giúp tính toán cạnh huyền không?
Trả lời: Có nhiều phần mềm và ứng dụng toán học có thể giúp bạn tính toán cạnh huyền một cách nhanh chóng. -
Câu hỏi: Tôi có thể hỏi ai nếu tôi gặp khó khăn trong việc áp dụng công thức tính cạnh huyền?
Trả lời: Bạn có thể hỏi giáo viên toán, bạn bè, hoặc tìm kiếm sự hỗ trợ từ các diễn đàn toán học trực tuyến.