Công Thức Tính Cos Góc là một trong những công cụ toán học cơ bản và quan trọng nhất, được ứng dụng rộng rãi trong nhiều lĩnh vực, từ vật lý đến đồ họa máy tính. Bài viết này sẽ giúp bạn hiểu rõ về công thức tính cos, cách áp dụng và những bí mật xoay quanh nó. bảng công thức sin cos
Định Nghĩa Cos Góc Trong Tam Giác Vuông
Trong tam giác vuông, cos của một góc nhọn được định nghĩa là tỷ số giữa cạnh kề của góc đó với cạnh huyền. Ví dụ, trong tam giác vuông ABC, với góc A là góc vuông, cos của góc B được tính bằng AB/BC. Điều này có nghĩa là nếu bạn biết độ dài của cạnh kề và cạnh huyền, bạn có thể dễ dàng tính được cos của góc đó.
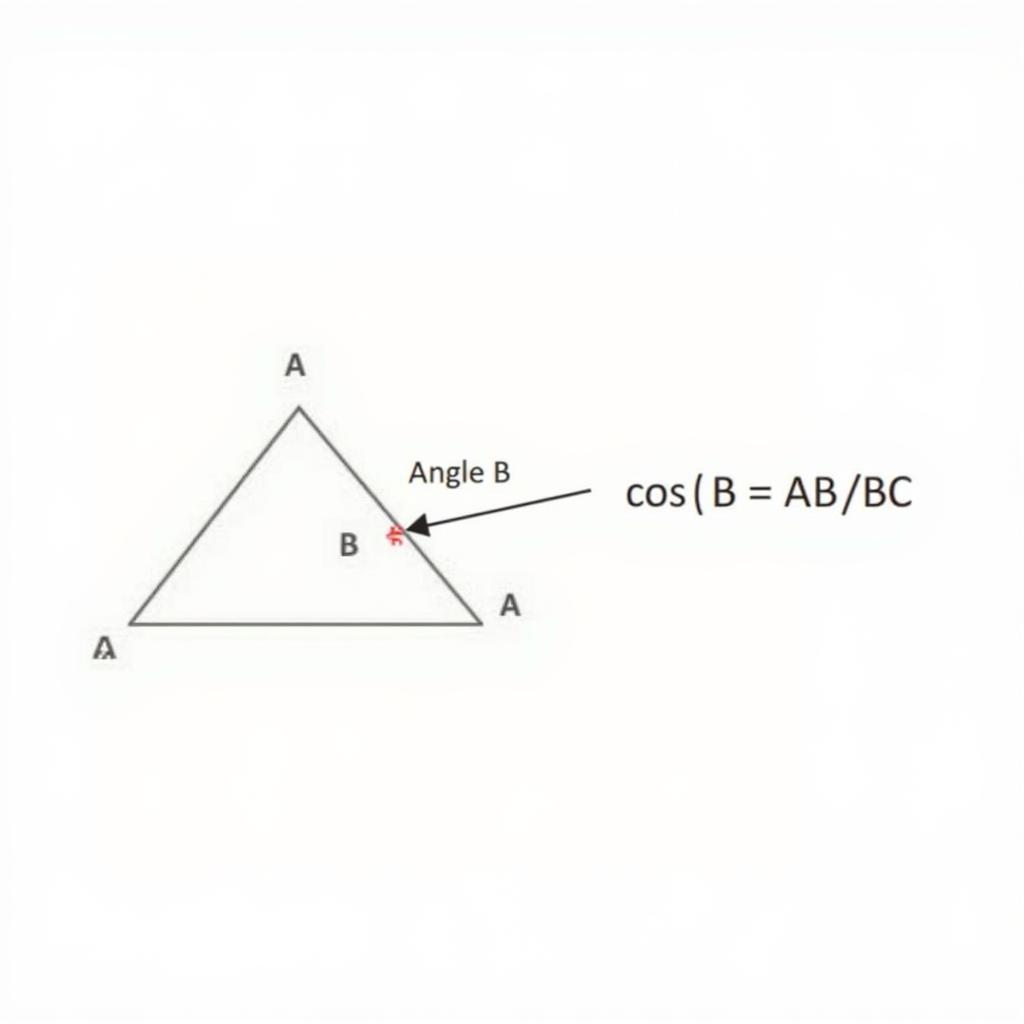 Định nghĩa cos góc trong tam giác vuông
Định nghĩa cos góc trong tam giác vuông
Công Thức Tính Cos Góc Trong Đường Tròn Lượng Giác
Trong đường tròn lượng giác, cos của một góc được định nghĩa là hoành độ của điểm trên đường tròn tương ứng với góc đó. Đường tròn lượng giác cung cấp một cách trực quan để hiểu mối quan hệ giữa góc và hàm cos.
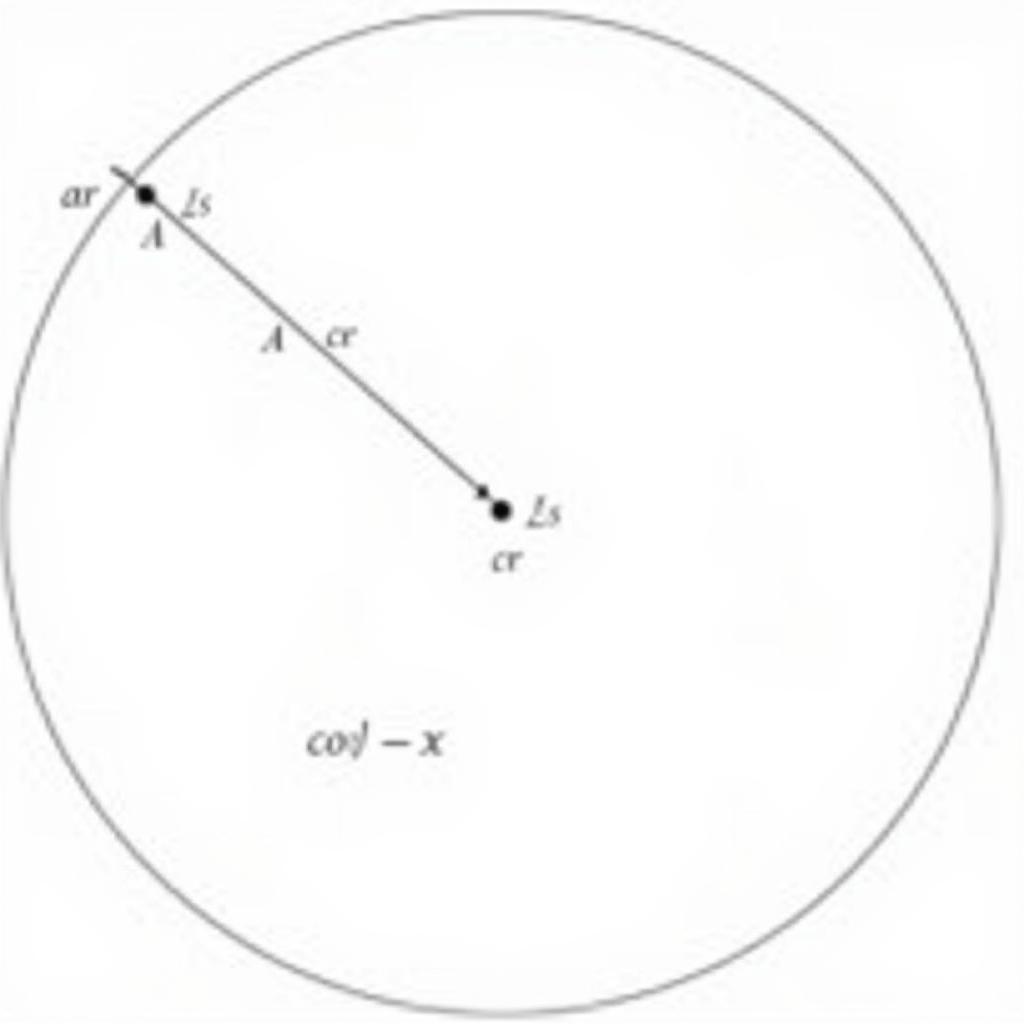 Công thức tính cos góc trong đường tròn lượng giác
Công thức tính cos góc trong đường tròn lượng giác
Các Công Thức Cos Góc Phổ Biến
Có rất nhiều công thức liên quan đến cos góc, bao gồm công thức cộng, công thức gấp đôi, công thức hạ bậc, và nhiều công thức khác. Việc nắm vững các công thức này sẽ giúp bạn giải quyết các bài toán liên quan đến cos góc một cách hiệu quả. công thức tính sin
Công Thức Cộng Cos
cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
Công Thức Gấp Đôi Cos
cos(2a) = cos²(a) – sin²(a) = 2cos²(a) – 1 = 1 – 2sin²(a)
Công Thức Hạ Bậc Cos
cos²(a) = (1 + cos(2a))/2
What “công thức tính cos góc”
Công thức tính cos góc là một tập hợp các phương trình toán học được sử dụng để tính giá trị cos của một góc, dựa trên các thông tin khác như cạnh kề, cạnh huyền, hoặc các góc khác.
Who “công thức tính cos góc”
Học sinh, sinh viên, kỹ sư, nhà khoa học, và bất kỳ ai làm việc trong lĩnh vực liên quan đến toán học và khoa học đều sử dụng công thức tính cos góc.
When “công thức tính cos góc”
Công thức tính cos góc được sử dụng khi cần tính toán các giá trị liên quan đến góc trong tam giác, đường tròn, hoặc các hình học khác, cũng như trong các ứng dụng vật lý và kỹ thuật.
Where “công thức tính cos góc”
Công thức tính cos góc được áp dụng trong nhiều lĩnh vực, bao gồm toán học, vật lý, kỹ thuật, đồ họa máy tính, và nhiều lĩnh vực khác.
Why “công thức tính cos góc”
Công thức tính cos góc là cần thiết để giải quyết các bài toán liên quan đến góc, hình học, và lượng giác, giúp chúng ta hiểu và mô tả thế giới xung quanh.
How “công thức tính cos góc”
Để tính cos góc, bạn có thể sử dụng các công thức đã được định nghĩa, máy tính, hoặc bảng giá trị lượng giác. các công thức hình học 11
Ông Nguyễn Văn A, Giáo sư Toán học tại Đại học X, chia sẻ: “Công thức tính cos góc không chỉ là một công cụ toán học khô khan, mà còn là chìa khóa để mở ra nhiều bí mật của vũ trụ. Từ việc tính toán quỹ đạo của các hành tinh đến việc thiết kế các công trình kiến trúc, công thức này đều đóng vai trò quan trọng.”
Bà Trần Thị B, Kỹ sư xây dựng, cho biết: “Trong công việc của tôi, công thức tính cos góc là một công cụ không thể thiếu. Nó giúp tôi tính toán chính xác các góc và khoảng cách trong các công trình xây dựng, đảm bảo sự an toàn và hiệu quả.”
Kết luận
Công thức tính cos góc là một kiến thức nền tảng quan trọng trong toán học và có ứng dụng rộng rãi trong đời sống. Hiểu rõ về công thức này sẽ giúp bạn giải quyết nhiều bài toán phức tạp và mở ra cánh cửa đến với thế giới toán học đầy thú vị. công thức đường cao tam giác cân
FAQ
-
Câu hỏi 1: Cos góc là gì?
-
Trả lời: Cos góc là tỷ số giữa cạnh kề và cạnh huyền trong tam giác vuông, hoặc là hoành độ của điểm trên đường tròn lượng giác tương ứng với góc đó.
-
Câu hỏi 2: Làm thế nào để tính cos góc?
-
Trả lời: Bạn có thể sử dụng các công thức cos, máy tính, hoặc bảng giá trị lượng giác.
-
Câu hỏi 3: Ứng dụng của công thức tính cos góc là gì?
-
Trả lời: Công thức tính cos góc được ứng dụng trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, đồ họa máy tính, v.v.
-
Câu hỏi 4: Công thức cộng cos là gì?
-
Trả lời: cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
-
Câu hỏi 5: Công thức gấp đôi cos là gì?
-
Trả lời: cos(2a) = cos²(a) – sin²(a) = 2cos²(a) – 1 = 1 – 2sin²(a)
-
Câu hỏi 6: Công thức hạ bậc cos là gì?
-
Trả lời: cos²(a) = (1 + cos(2a))/2
-
Câu hỏi 7: Đường tròn lượng giác là gì?
-
Trả lời: Đường tròn lượng giác là một đường tròn có bán kính bằng 1, được sử dụng để biểu diễn các góc và hàm lượng giác.
-
Câu hỏi 8: Làm sao để nhớ các công thức cos?
-
Trả lời: Bạn có thể học thuộc lòng, sử dụng các mẹo ghi nhớ, hoặc luyện tập thường xuyên. công thức tích phân nâng cao
-
Câu hỏi 9: Cos của góc 0 độ là bao nhiêu?
-
Trả lời: Cos của góc 0 độ là 1.
-
Câu hỏi 10: Cos của góc 90 độ là bao nhiêu?
-
Trả lời: Cos của góc 90 độ là 0.
