Công thức tính thể tích tứ diện trong Oxyz là một kiến thức quan trọng trong hình học không gian. Nắm vững công thức này giúp bạn giải quyết nhiều bài toán phức tạp một cách dễ dàng và hiệu quả. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về công thức tính thể tích tứ diện, từ cơ bản đến nâng cao, cùng với những ví dụ minh họa cụ thể. công thức toán hình học không gian lớp 12
Định Nghĩa Tứ Diện và Các Yếu Tố Liên Quan
Tứ diện là một hình không gian được tạo bởi bốn điểm không đồng phẳng. Bốn điểm này được gọi là các đỉnh của tứ diện. Tứ diện có sáu cạnh và bốn mặt, mỗi mặt là một tam giác. Để tính thể tích tứ diện, ta cần nắm rõ các khái niệm như vectơ, tọa độ điểm trong không gian Oxyz, tích có hướng của hai vectơ.
Tọa Độ Đỉnh và Vectơ
Trong không gian Oxyz, mỗi đỉnh của tứ diện được xác định bởi ba tọa độ (x, y, z). Từ tọa độ các đỉnh, ta có thể xác định các vectơ tạo bởi các cạnh của tứ diện. Ví dụ, nếu tứ diện ABCD có tọa độ các đỉnh lần lượt là A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC), và D(xD, yD, zD), thì vectơ AB được tính bằng (xB – xA, yB – yA, zB – zA).
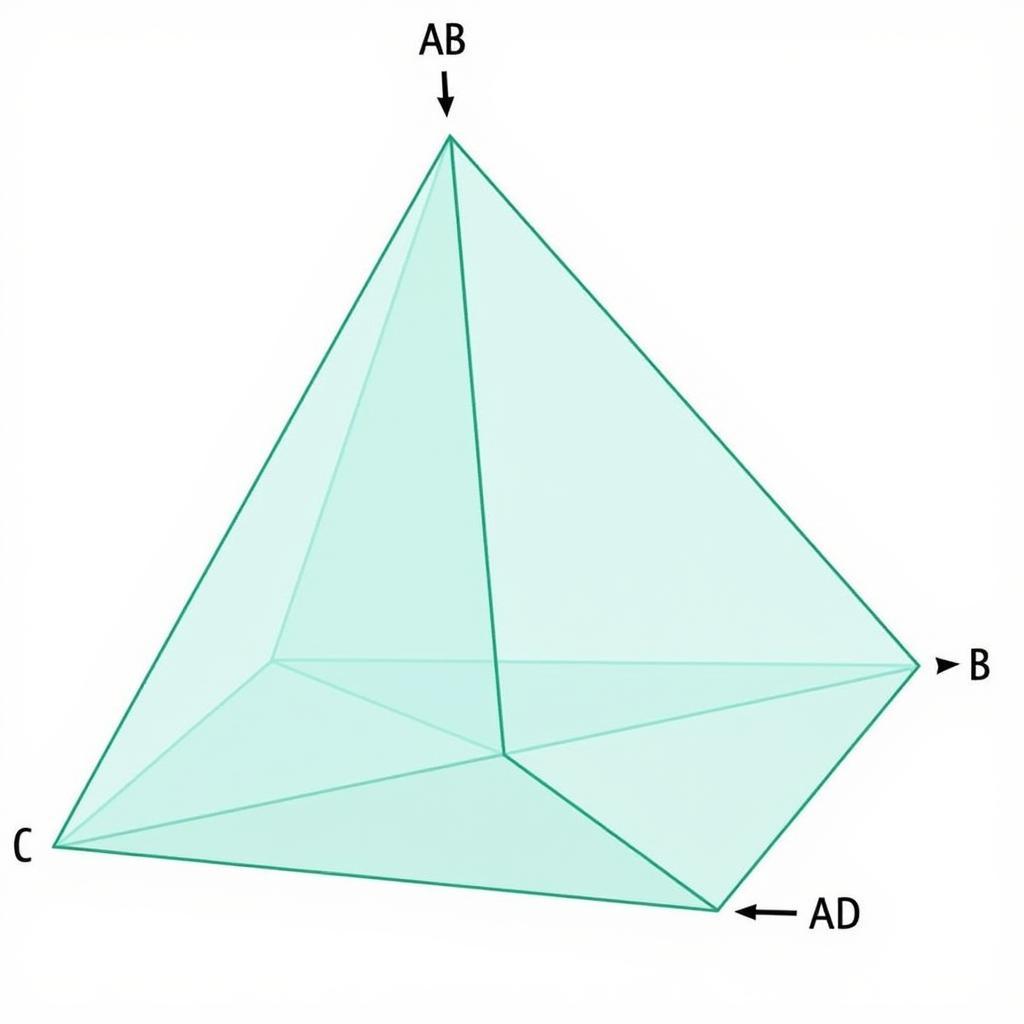Tính Thể Tích Tứ Diện Trong Không Gian Oxyz
Công Thức Tính Thể Tích Tứ Diện
Công thức tính thể tích tứ diện ABCD được cho bởi:
V = 1/6 |[AB, AC, AD]|Trong đó:
- AB, AC, AD là các vectơ được tạo bởi các cạnh của tứ diện xuất phát từ cùng một đỉnh (ở đây là đỉnh A).
- [AB, AC, AD] là tích hỗn tạp của ba vectơ AB, AC, và AD.
- |[AB, AC, AD]| là giá trị tuyệt đối của tích hỗn tạp.
Cách Tính Tích Hỗn Tạp
Tích hỗn tạp [AB, AC, AD] được tính bằng cách tính định thức của ma trận có các hàng là tọa độ của các vectơ AB, AC, và AD. công thức đo độ dài
[AB, AC, AD] = | xAB yAB zAB |
| xAC yAC zAC |
| xAD yAD zAD |Ví Dụ Minh Họa
Cho tứ diện ABCD với A(1, 2, 3), B(2, 1, 4), C(3, 0, 1), và D(0, 4, 2). Tính thể tích tứ diện ABCD.
Giải:
-
Tính các vectơ:
AB = (1, -1, 1)
AC = (2, -2, -2)
AD = (-1, 2, -1) -
Tính tích hỗn tạp:
[AB, AC, AD] = | 1 -1 1 |
| 2 -2 -2 |
| -1 2 -1 |
= 1*(-2*-1 - (-2)*2) - (-1)*(2*-1 - (-2)*-1) + 1*(2*2 - (-2)*-1)
= 6 + 4 + 2 = 12- Tính thể tích:
V = 1/6 * |12| = 2
Vậy thể tích tứ diện ABCD là 2 đơn vị thể tích.
Trả Lời Các Câu Hỏi
What “công thức tính thể tích tứ diện trong oxyz”? Công thức là V = 1/6 |[AB, AC, AD]| với AB, AC, AD là vectơ cạnh.
Who “công thức tính thể tích tứ diện trong oxyz”? Học sinh, sinh viên, và những người làm việc trong lĩnh vực liên quan đến hình học không gian cần biết công thức này.
When “công thức tính thể tích tứ diện trong oxyz”? Công thức này được sử dụng khi cần tính thể tích của một tứ diện trong không gian Oxyz. công thức khoảng cách
Where “công thức tính thể tích tứ diện trong oxyz”? Công thức này được áp dụng trong hình học không gian, toán học, vật lý, và các lĩnh vực liên quan.
Why “công thức tính thể tích tứ diện trong oxyz”? Công thức này giúp tính toán thể tích tứ diện một cách chính xác và hiệu quả.
How “công thức tính thể tích tứ diện trong oxyz”? Tính toán bằng cách tìm các vectơ cạnh, tính tích hỗn tạp, và áp dụng công thức. công thức tính độ dài đoạn thẳng trong oxyz
Bổ sung trích dẫn từ chuyên gia giả định:
Theo Tiến sĩ Nguyễn Văn Toán, chuyên gia hàng đầu về Hình học Không gian: “Việc nắm vững công thức tính thể tích tứ diện trong Oxyz là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong hình học không gian.”
Ông cũng nhấn mạnh: “Ứng dụng của công thức này không chỉ giới hạn trong toán học mà còn mở rộng sang nhiều lĩnh vực khác như vật lý, kỹ thuật, và đồ họa máy tính.”
Ứng Dụng Công Thức Tính Thể Tích Tứ Diện
Kết luận
Công thức tính thể tích tứ diện trong Oxyz là một công cụ hữu ích và cần thiết trong việc giải quyết các bài toán hình học không gian. Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ và chi tiết về công thức tính thể tích tứ diện trong oxyz. công thức hình chiếu trong tam giác vuông
FAQ
1. Nêu Câu Hỏi: Tích hỗn tạp là gì?
Trả Lời Chi tiết Câu Hỏi: Tích hỗn tạp của ba vectơ là một đại lượng vô hướng, được tính bằng định thức của ma trận tạo bởi tọa độ của ba vectơ đó.
2. Nêu Câu Hỏi: Làm thế nào để tìm vectơ từ tọa độ các điểm?
Trả Lời Chi tiết Câu Hỏi: Vectơ AB được tính bằng cách lấy tọa độ điểm B trừ đi tọa độ điểm A.
3. Nêu Câu Hỏi: Công thức tính thể tích tứ diện có áp dụng cho tam giác không?
Trả Lời Chi tiết Câu Hỏi: Không, công thức này chỉ áp dụng cho tứ diện. Tam giác là hình phẳng, còn tứ diện là hình không gian.
4. Nêu Câu Hỏi: Có cách nào khác để tính thể tích tứ diện không?
Trả Lời Chi tiết Câu Hỏi: Có, có thể sử dụng phương pháp chia tứ diện thành các hình chóp nhỏ hơn để tính thể tích.
5. Nêu Câu Hỏi: Giá trị tuyệt đối trong công thức thể tích có ý nghĩa gì?
Trả Lời Chi tiết Câu Hỏi: Giá trị tuyệt đối đảm bảo thể tích luôn là một số dương.
6. Nêu Câu Hỏi: Ứng dụng của công thức này trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Ứng dụng trong xây dựng, thiết kế, và nhiều lĩnh vực khoa học khác.
7. Nêu Câu Hỏi: Nếu tứ diện có một đỉnh trùng với gốc tọa độ thì công thức tính thể tích có thay đổi không?
Trả Lời Chi tiết Câu Hỏi: Không, công thức vẫn giữ nguyên. Việc một đỉnh trùng gốc tọa độ chỉ làm cho việc tính toán các vectơ đơn giản hơn.
8. Nêu Câu Hỏi: Làm thế nào để nhớ công thức này dễ dàng hơn?
Trả Lời Chi tiết Câu Hỏi: Liên hệ công thức với hình ảnh hình học và thực hành nhiều bài tập.
9. Nêu Câu Hỏi: Tích hỗn tạp có tính chất gì đặc biệt?
Trả Lời Chi tiết Câu Hỏi: Tích hỗn tạp có tính chất hoán vị vòng quanh.
10. Nêu Câu Hỏi: Nếu ba vectơ đồng phẳng thì tích hỗn tạp bằng bao nhiêu?
Trả Lời Chi tiết Câu Hỏi: Nếu ba vectơ đồng phẳng thì tích hỗn tạp bằng 0.