Công Thức Tính Tỉ Số Lượng Giác là nền tảng quan trọng trong toán học, đặc biệt là hình học và lượng giác. Nắm vững các công thức này không chỉ giúp bạn giải quyết các bài toán phức tạp mà còn mở ra cánh cửa khám phá thế giới toán học đầy bí ẩn. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về công thức tính tỉ số lượng giác, từ cơ bản đến nâng cao, cùng với những ví dụ thực tế và lời khuyên hữu ích.
Tìm Hiểu Về Tỉ Số Lượng Giác
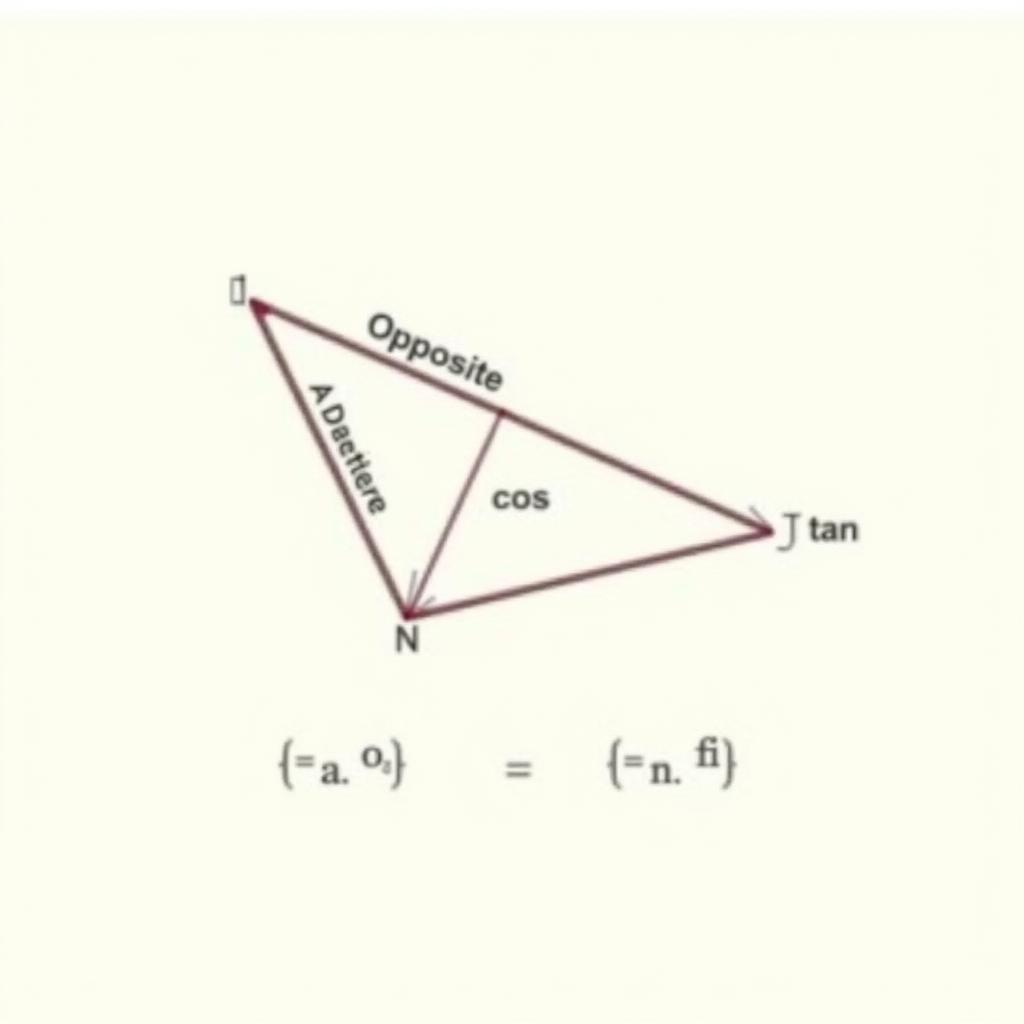
Tỉ số lượng giác của một góc nhọn trong tam giác vuông được định nghĩa là tỉ số giữa hai cạnh của tam giác đó. Có sáu tỉ số lượng giác cơ bản: sin, cos, tan, cot, sec, và cosec. Chúng ta sẽ cùng tìm hiểu chi tiết về từng tỉ số và mối quan hệ giữa chúng.
- Sin (sin α): Tỉ số giữa cạnh đối và cạnh huyền.
- Cosin (cos α): Tỉ số giữa cạnh kề và cạnh huyền.
- Tang (tan α): Tỉ số giữa cạnh đối và cạnh kề.
- Cotang (cot α): Tỉ số giữa cạnh kề và cạnh đối.
- Sec (sec α): Tỉ số giữa cạnh huyền và cạnh kề.
- Cosec (cosec α): Tỉ số giữa cạnh huyền và cạnh đối.
 Công Thức Tỉ Số Lượng Giác Cơ Bản
Công Thức Tỉ Số Lượng Giác Cơ Bản
Công Thức Tính Tỉ Số Lượng Giác Cơ Bản
Dưới đây là công thức tính tỉ số lượng giác cơ bản cho góc nhọn α trong tam giác vuông ABC, với góc vuông tại C:
- sin α = BC/AB
- cos α = AC/AB
- tan α = BC/AC
- cot α = AC/BC
- sec α = AB/AC
- cosec α = AB/BC
Các công thức này là nền tảng để xây dựng các công thức phức tạp hơn. Việc ghi nhớ và áp dụng thành thạo chúng sẽ giúp bạn giải quyết nhiều bài toán hình học.
Bạn đã bao giờ tự hỏi làm thế nào để tính toán đường trung tuyến của một tam giác? Hãy xem bài viết về chứng minh công thức tính đường trung tuyến để hiểu rõ hơn.
Mối Quan Hệ Giữa Các Tỉ Số Lượng Giác
Các tỉ số lượng giác không tồn tại độc lập mà có mối liên hệ chặt chẽ với nhau. Dưới đây là một số mối quan hệ quan trọng:
- tan α = sin α / cos α
- cot α = cos α / sin α
- cot α = 1 / tan α
- sec α = 1 / cos α
- cosec α = 1 / sin α
What Công Thức Tính Tỉ Số Lượng Giác?
Công thức tính tỉ số lượng giác là các công thức toán học dùng để tính toán các tỉ số lượng giác của một góc, thường là trong tam giác vuông.
Who Sử Dụng Công Thức Tính Tỉ Số Lượng Giác?
Học sinh, sinh viên, kỹ sư, nhà khoa học, và bất kỳ ai làm việc trong lĩnh vực liên quan đến toán học và khoa học đều sử dụng công thức tính tỉ số lượng giác.
When Sử Dụng Công Thức Tính Tỉ Số Lượng Giác?
Công thức tính tỉ số lượng giác được sử dụng khi cần tính toán các giá trị liên quan đến góc và cạnh trong tam giác vuông, cũng như trong nhiều ứng dụng khác của toán học và khoa học.
Where Áp Dụng Công Thức Tính Tỉ Số Lượng Giác?
Công thức tính tỉ số lượng giác được áp dụng rộng rãi trong hình học, vật lý, thiên văn học, kỹ thuật, và nhiều lĩnh vực khác.
Why Học Công Thức Tính Tỉ Số Lượng Giác Quan Trọng?
Hiểu và áp dụng công thức tính tỉ số lượng giác là rất quan trọng để giải quyết các bài toán liên quan đến góc và hình học, cũng như để hiểu sâu hơn về các khái niệm toán học và khoa học khác.
How Ghi Nhớ Công Thức Tính Tỉ Số Lượng Giác?
Có nhiều cách để ghi nhớ công thức tính tỉ số lượng giác, bao gồm sử dụng các mẹo ghi nhớ, thực hành giải bài tập, và sử dụng các công cụ trực quan.
Có thể bạn quan tâm đến các công thức bấm máy tính để giải toán nhanh hơn.
“Việc nắm vững công thức tính tỉ số lượng giác là chìa khóa để mở ra cánh cửa vào thế giới toán học đầy thú vị,” – Nguyễn Văn A, Giáo sư Toán học, Đại học Quốc gia Hà Nội.
“Không chỉ trong toán học, tỉ số lượng giác còn có ứng dụng rộng rãi trong cuộc sống hàng ngày, từ việc xây dựng nhà cửa đến thiết kế máy móc,” – Trần Thị B, Kỹ sư Xây dựng.
Nếu bạn đang tìm hiểu về các công thức hóa học, hãy xem bài viết về công thức hóa học của aspirin.
Kết luận
Công thức tính tỉ số lượng giác là một phần không thể thiếu trong toán học. Hiểu rõ và vận dụng thành thạo các công thức này sẽ giúp bạn giải quyết nhiều bài toán khó và mở ra cánh cửa khám phá những khía cạnh thú vị của toán học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về công thức tính tỉ số lượng giác.
FAQ
-
Nêu Câu Hỏi: Tỉ số lượng giác là gì?
Trả Lời Chi tiết Câu Hỏi: Tỉ số lượng giác là tỉ số giữa hai cạnh của một tam giác vuông, liên quan đến một góc nhọn cụ thể. -
Nêu Câu Hỏi: Có bao nhiêu tỉ số lượng giác cơ bản?
Trả Lời Chi tiết Câu Hỏi: Có sáu tỉ số lượng giác cơ bản: sin, cos, tan, cot, sec và cosec. -
Nêu Câu Hỏi: Làm thế nào để tính tan α?
Trả Lời Chi tiết Câu Hỏi: tan α được tính bằng tỉ số giữa cạnh đối và cạnh kề của góc α trong tam giác vuông. -
Nêu Câu Hỏi: Mối quan hệ giữa sin α và cosec α là gì?
Trả Lời Chi tiết Câu Hỏi: cosec α là nghịch đảo của sin α, tức là cosec α = 1/sin α. -
Nêu Câu Hỏi: Ứng dụng của công thức tính tỉ số lượng giác trong thực tế là gì?
Trả Lời Chi tiết Câu Hỏi: Công thức tính tỉ số lượng giác được ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, đo đạc, định vị, vật lý, và thiên văn học. -
Nêu Câu Hỏi: Làm thế nào để học tốt công thức tính tỉ số lượng giác?
Trả Lời Chi tiết Câu Hỏi: Học tốt công thức tính tỉ số lượng giác bằng cách luyện tập thường xuyên, hiểu rõ định nghĩa và mối quan hệ giữa các tỉ số. -
Nêu Câu Hỏi: Có tài liệu nào hỗ trợ học công thức tính tỉ số lượng giác không?
Trả Lời Chi tiết Câu Hỏi: Có rất nhiều sách giáo khoa, website, và video hướng dẫn về công thức tính tỉ số lượng giác. -
Nêu Câu Hỏi: Công thức tính tỉ số lượng giác có liên quan đến góc nào trong tam giác vuông?
Trả Lời Chi tiết Câu Hỏi: Công thức tính tỉ số lượng giác liên quan đến các góc nhọn trong tam giác vuông. -
Nêu Câu Hỏi: Tỉ số lượng giác có áp dụng cho tam giác không vuông không?
Trả Lời Chi tiết Câu Hỏi: Có, tuy nhiên, việc tính toán sẽ phức tạp hơn và thường sử dụng định luật sin và cos. -
Nêu Câu Hỏi: Làm thế nào để nhớ nhanh các công thức tính tỉ số lượng giác?
Trả Lời Chi tiết Câu Hỏi: Có nhiều mẹo ghi nhớ, ví dụ như sử dụng câu thần chú “SOH CAH TOA” (Sin = Opposite/Hypotenuse, Cos = Adjacent/Hypotenuse, Tan = Opposite/Adjacent). Tìm hiểu thêm về công thức axit lactic. Ngoài ra, việc làm bài tập thường xuyên cũng giúp ghi nhớ công thức hiệu quả. Tham khảo thêm tài liệu về công phá bất đẳng thức pdf để nâng cao kiến thức.
