Công Thức Tính Tổng Dãy Số Cách đều là một kiến thức toán học cơ bản nhưng vô cùng hữu ích, được áp dụng rộng rãi trong nhiều lĩnh vực từ học thuật đến đời sống. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về công thức này, từ cách hiểu đơn giản đến ứng dụng phức tạp. công thức câu bị động
Hiểu Về Dãy Số Cách Đều và Công Thức Tính Tổng
Dãy số cách đều là dãy số mà hiệu giữa hai số hạng liên tiếp luôn bằng một hằng số, gọi là công sai (d). Ví dụ, dãy số 2, 4, 6, 8 là một dãy số cách đều với công sai d = 2. Để tính tổng của một dãy số cách đều, chúng ta sử dụng công thức: S = (n/2) * [2a + (n-1)d], trong đó S là tổng của dãy số, n là số số hạng, a là số hạng đầu tiên, và d là công sai.
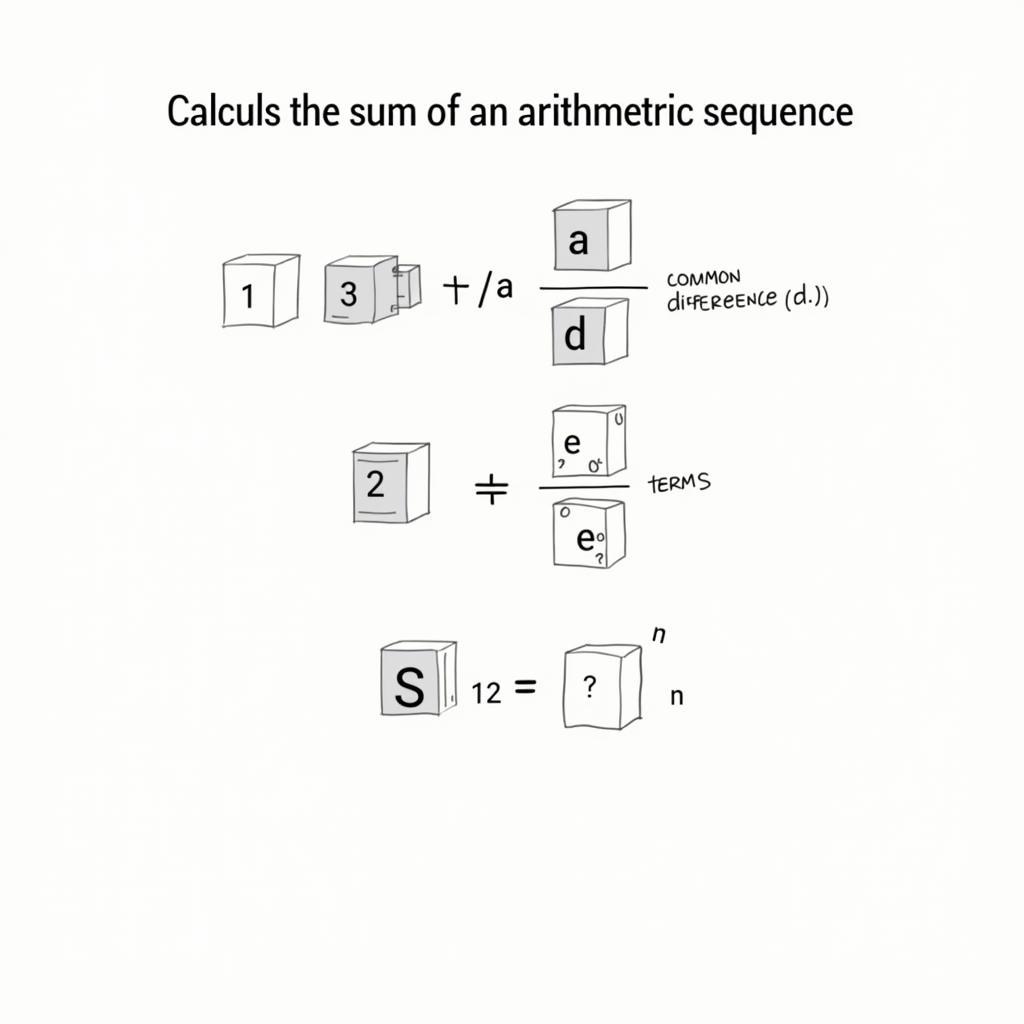Công thức tính tổng dãy số cách đều minh họa
Ứng Dụng Của Công Thức Tính Tổng Dãy Số Cách Đều Trong Đời Sống
Công thức này không chỉ giới hạn trong sách vở mà còn được ứng dụng rộng rãi trong thực tế. Từ việc tính toán lãi suất ngân hàng, dự đoán doanh thu, đến thiết kế kiến trúc và lập trình máy tính, công thức tính tổng dãy số cách đều đều đóng vai trò quan trọng. Ví dụ, một người gửi tiết kiệm hàng tháng với số tiền cố định tăng dần theo một dãy số cách đều, có thể dễ dàng tính được tổng số tiền tiết kiệm sau một khoảng thời gian nhất định.
Tính Tổng Dãy Số Cách Đều Với Số Hạng Đầu Tiên và Số Hạng Cuối Cùng
Một biến thể khác của công thức tính tổng dãy số cách đều là sử dụng số hạng đầu tiên (a) và số hạng cuối cùng (l): S = (n/2) * (a + l). Công thức này đặc biệt hữu ích khi ta biết số hạng cuối cùng mà không cần tính công sai.
Tính tổng dãy số cách đều với số hạng cuối
What công thức tính tổng dãy số cách đều?
Công thức tính tổng dãy số cách đều là phương pháp toán học để tính tổng của một chuỗi số có khoảng cách giữa các số hạng liên tiếp là bằng nhau.
Who công thức tính tổng dãy số cách đều?
Học sinh, sinh viên, kỹ sư, nhà khoa học, và bất kỳ ai làm việc với dữ liệu số đều sử dụng công thức này.
When công thức tính tổng dãy số cách đều?
Công thức này được sử dụng khi cần tính tổng của một dãy số có quy luật cách đều.
Where công thức tính tổng dãy số cách đều?
Công thức này được áp dụng trong nhiều lĩnh vực, từ toán học, vật lý, đến kinh tế và khoa học máy tính. công thức nhuộm màu nâu tây trên nền tóc đen
Why công thức tính tổng dãy số cách đều?
Công thức này giúp tiết kiệm thời gian và công sức so với việc cộng từng số hạng một, đặc biệt là với dãy số có nhiều số hạng.
How công thức tính tổng dãy số cách đều?
Sử dụng công thức S = (n/2) [2a + (n-1)d] hoặc S = (n/2) (a + l) để tính tổng.
Theo Nguyễn Văn A, Tiến sĩ Toán học, “Công thức tính tổng dãy số cách đều là một công cụ toán học cơ bản nhưng mạnh mẽ, giúp đơn giản hóa nhiều bài toán phức tạp.”
Ứng dụng công thức tính tổng dãy số cách đều
Công thức tính tổng dãy số cách đều là một công cụ toán học quan trọng và hữu ích. Hiểu rõ về công thức này và cách áp dụng nó sẽ giúp bạn giải quyết nhiều bài toán trong học tập và cuộc sống. công thức tính diện tích tam giác lớp 9 đá vôi công thức Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về công thức tính tổng dãy số cách đều. công thức điện trở r
FAQ
1. Nêu Câu Hỏi: Dãy số nào là dãy số cách đều?
Trả Lời Chi tiết Câu Hỏi: Dãy số mà hiệu giữa hai số hạng liên tiếp luôn bằng một hằng số.
2. Nêu Câu Hỏi: Công sai là gì?
Trả Lời Chi tiết Câu Hỏi: Công sai là hiệu giữa hai số hạng liên tiếp trong dãy số cách đều.
3. Nêu Câu Hỏi: Công thức tính tổng dãy số cách đều là gì?
Trả Lời Chi tiết Câu Hỏi: S = (n/2) [2a + (n-1)d] hoặc S = (n/2) (a + l).
*4. Nêu Câu Hỏi: Khi nào nên sử dụng công thức S = (n/2) (a + l)?
Trả Lời Chi tiết Câu Hỏi:** Khi biết số hạng đầu tiên và số hạng cuối cùng của dãy.
5. Nêu Câu Hỏi: Ứng dụng của công thức tính tổng dãy số cách đều trong thực tế?
Trả Lời Chi tiết Câu Hỏi: Tính toán lãi suất, dự đoán doanh thu, thiết kế kiến trúc, lập trình máy tính, v.v.
6. Nêu Câu Hỏi: Làm thế nào để xác định số số hạng (n) trong dãy?
Trả Lời Chi tiết Câu Hỏi: Có thể đếm trực tiếp hoặc sử dụng công thức nếu biết số hạng đầu, cuối và công sai.
7. Nêu Câu Hỏi: Nếu công sai là số âm thì sao?
Trả Lời Chi tiết Câu Hỏi: Công thức vẫn áp dụng bình thường.
8. Nêu Câu Hỏi: Có công cụ nào hỗ trợ tính tổng dãy số cách đều không?
Trả Lời Chi tiết Câu Hỏi: Có, nhiều máy tính và phần mềm toán học có thể tính toán này.
9. Nêu Câu Hỏi: Tôi có thể tìm hiểu thêm về dãy số cách đều ở đâu?
Trả Lời Chi tiết Câu Hỏi: Sách giáo khoa toán học, website giáo dục, hoặc các khóa học online.
10. Nêu Câu Hỏi: Có những loại dãy số đặc biệt nào khác không?
Trả Lời Chi tiết Câu Hỏi: Có, ví dụ như dãy số cấp số nhân, dãy Fibonacci.