Công Thức Tính Vectơ: Hướng Dẫn Chi Tiết Từ A Đến Z

Công Thức Tính Vectơ là nền tảng của toán học và vật lý, giúp chúng ta mô tả và phân tích các đại lượng có cả độ lớn và hướng. Từ việc tính toán lực tác động lên một vật thể đến việc mô hình hóa chuyển động của các hạt, công thức tính vectơ đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về các công thức tính vectơ quan trọng, từ cơ bản đến nâng cao.

Khái Niệm Cơ Bản Về Vectơ

Trước khi đi sâu vào các công thức, hãy cùng ôn lại khái niệm cơ bản về vectơ. Vectơ là một đại lượng có cả độ lớn và hướng. Nó được biểu diễn bằng một mũi tên, với độ dài mũi tên thể hiện độ lớn và hướng mũi tên thể hiện hướng của vectơ. các công thức tính vecto giúp chúng ta thực hiện các phép toán trên các vectơ này.

Biểu Diễn Vectơ

Vectơ thường được biểu diễn bằng chữ cái in đậm, ví dụ a, b, v. Trong hệ tọa độ Descartes, một vectơ a có thể được biểu diễn bằng các thành phần của nó trên các trục tọa độ: a = (a_x, a_y, a_z).

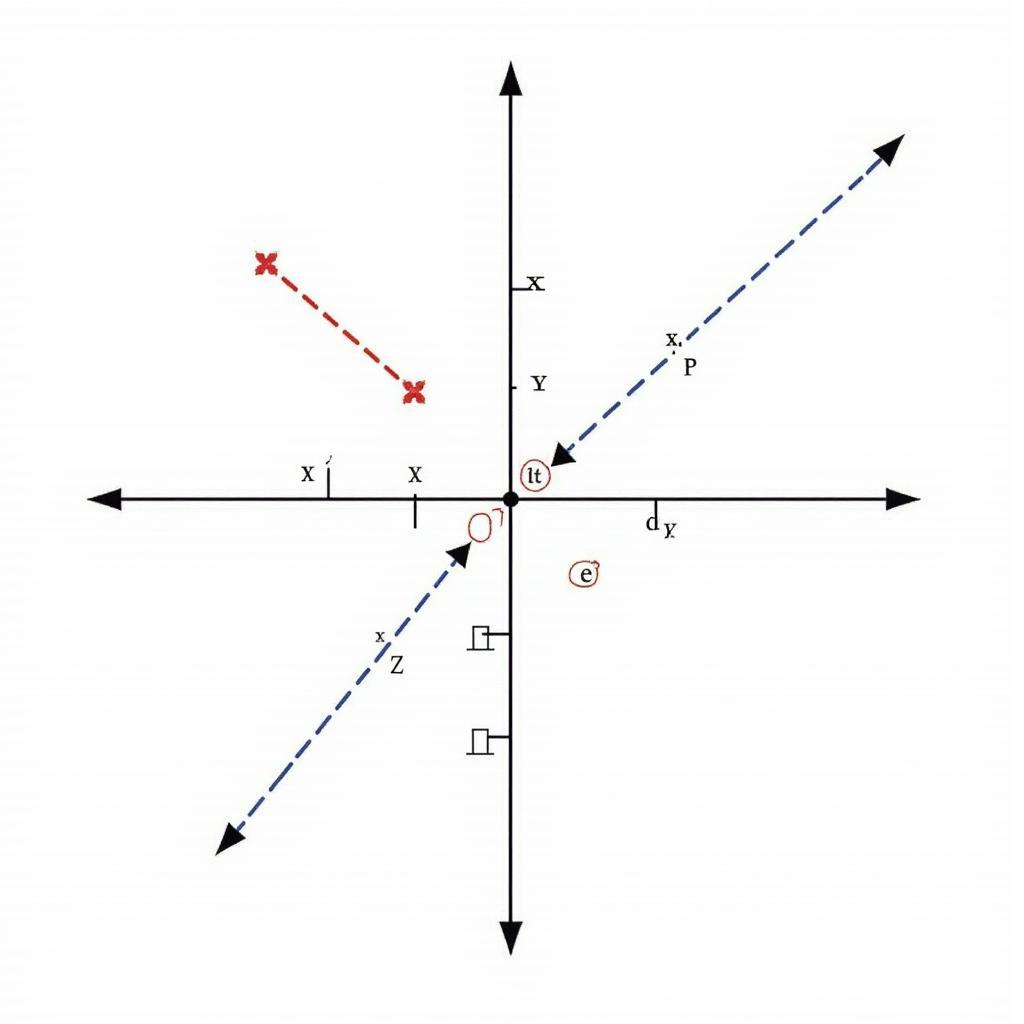Biểu diễn vectơ trong hệ tọa độ Descartes

Các Công Thức Tính Vectơ Quan Trọng

Dưới đây là một số công thức tính vectơ quan trọng mà bạn cần nắm vững:

Công Thức Tính Độ Dài Vectơ

Độ dài của vectơ a được ký hiệu là |a| và được tính bằng công thức: |a| = √(a_x² + a_y² + a_z²).

Công Thức Tính Tổng Và Hiệu Hai Vectơ

Tổng của hai vectơ a và b là một vectơ mới c = a + b, với c_x = a_x + b_x, c_y = a_y + b_y, và c_z = a_z + b_z. Tương tự, hiệu của hai vectơ a và b là c = a – b, với c_x = a_x – b_x, c_y = a_y – b_y, và c_z = a_z – b_z.

Công Thức Tính Tích Vô Hướng

Tích vô hướng của hai vectơ a và b được ký hiệu là a · b và được tính bằng công thức: a · b = |a| |b| cosθ, trong đó θ là góc giữa hai vectơ. công thức tính góc giữa 2 vecto sẽ được trình bày chi tiết hơn ở phần sau. Ngoài ra, tích vô hướng cũng có thể được tính bằng: a · b = a_xb_x + a_yb_y + a_zb_z.

Công Thức Tính Góc Giữa Hai Vectơ

Từ công thức tích vô hướng, ta có thể suy ra công thức tính góc giữa hai vectơ a và b: cosθ = (a · b) / (|a| |b|). công thức tính góc giữa hai vectơ này rất hữu ích trong nhiều bài toán.

Công Thức Tính Vectơ Pháp Tuyến Trong Không Gian

Trong không gian ba chiều, vectơ pháp tuyến của một mặt phẳng được xác định bởi tích có hướng của hai vectơ không cùng phương nằm trên mặt phẳng đó. công thức tính vecto pháp tuyến trong khong gian đóng vai trò quan trọng trong hình học không gian.

Vectơ pháp tuyến của mặt phẳng

Trả Lời Các Câu Hỏi

• What công thức tính vectơ? Công thức tính vectơ bao gồm các công thức tính độ dài, tổng, hiệu, tích vô hướng, tích có hướng, góc giữa hai vectơ, và nhiều phép toán khác.
• Who sử dụng công thức tính vectơ? Các nhà khoa học, kỹ sư, và học sinh trong lĩnh vực toán học, vật lý, và các lĩnh vực liên quan đều sử dụng công thức tính vectơ.
• When cần sử dụng công thức tính vectơ? Khi làm việc với các đại lượng có cả độ lớn và hướng, chẳng hạn như lực, vận tốc, và gia tốc.
• Where áp dụng công thức tính vectơ? Công thức tính vectơ được áp dụng rộng rãi trong vật lý, toán học, đồ họa máy tính, và nhiều lĩnh vực khác.
• Why công thức tính vectơ quan trọng? Chúng cung cấp công cụ toán học để mô tả và phân tích các hiện tượng trong thế giới thực.
• How sử dụng công thức tính vectơ? Cần hiểu rõ khái niệm vectơ và áp dụng đúng công thức tương ứng với bài toán.

Trích Dẫn Chuyên Gia

• GS.TS Nguyễn Văn A, Viện Toán học: “Công thức tính vectơ là nền tảng không thể thiếu trong toán học hiện đại, giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả.”
• PGS.TS Trần Thị B, Đại học Khoa học Tự nhiên: “Việc nắm vững các công thức tính vectơ là chìa khóa để thành công trong học tập và nghiên cứu các lĩnh vực khoa học kỹ thuật.”

Kết Luận

Công thức tính vectơ là một công cụ mạnh mẽ giúp chúng ta mô tả và phân tích các hiện tượng trong thế giới thực. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về các công thức tính vectơ quan trọng. Hãy tiếp tục luyện tập và áp dụng chúng vào các bài toán cụ thể để nâng cao kiến thức của mình. công thức tính độ dài vecto là một trong những công thức cơ bản nhất mà bạn nên nắm vững.

FAQ

1. Vectơ là gì? Vectơ là một đại lượng có cả độ lớn và hướng.
2. Làm thế nào để tính độ dài của một vectơ? Sử dụng công thức |a| = √(a_x² + a_y² + a_z²).
3. Tích vô hướng của hai vectơ là gì? Là một đại lượng vô hướng được tính bằng tích độ dài hai vectơ và cosin của góc giữa chúng.
4. Tích có hướng của hai vectơ là gì? Là một vectơ vuông góc với cả hai vectơ ban đầu.
5. Làm thế nào để tính góc giữa hai vectơ? Sử dụng công thức cosθ = (a · b) / (|a| |b|).
6. Vectơ đơn vị là gì? Là vectơ có độ dài bằng 1.
7. Ứng dụng của vectơ trong đời sống là gì? Vectơ được sử dụng rộng rãi trong vật lý, kỹ thuật, đồ họa máy tính, v.v.
8. Làm thế nào để biểu diễn vectơ trong không gian ba chiều? Sử dụng hệ tọa độ Descartes với ba thành phần (x, y, z).
9. Phân biệt giữa vectơ và đại lượng vô hướng? Đại lượng vô hướng chỉ có độ lớn, trong khi vectơ có cả độ lớn và hướng.
10. Tầm quan trọng của việc học về vectơ là gì? Vectơ là nền tảng cho nhiều khái niệm trong toán học và khoa học, giúp chúng ta hiểu và mô hình hóa thế giới xung quanh.