Công Thức Trị Tuyệt đối Lớp 10 là một trong những kiến thức nền tảng quan trọng của toán học, mở ra cánh cửa cho việc giải quyết nhiều bài toán phức tạp. Việc nắm vững khái niệm và các công thức liên quan sẽ giúp bạn tự tin hơn trong hành trình chinh phục toán học.
Định Nghĩa Trị Tuyệt Đối và Ý Nghĩa Của Nó
Trị tuyệt đối của một số thực x, ký hiệu là |x|, được định nghĩa là khoảng cách từ điểm x đến điểm 0 trên trục số. Nói cách khác, trị tuyệt đối của một số luôn là một số không âm. |x| = x nếu x ≥ 0 và |x| = -x nếu x < 0. Hiểu rõ định nghĩa này sẽ giúp bạn dễ dàng áp dụng công thức trị tuyệt đối lớp 10 vào thực tế.
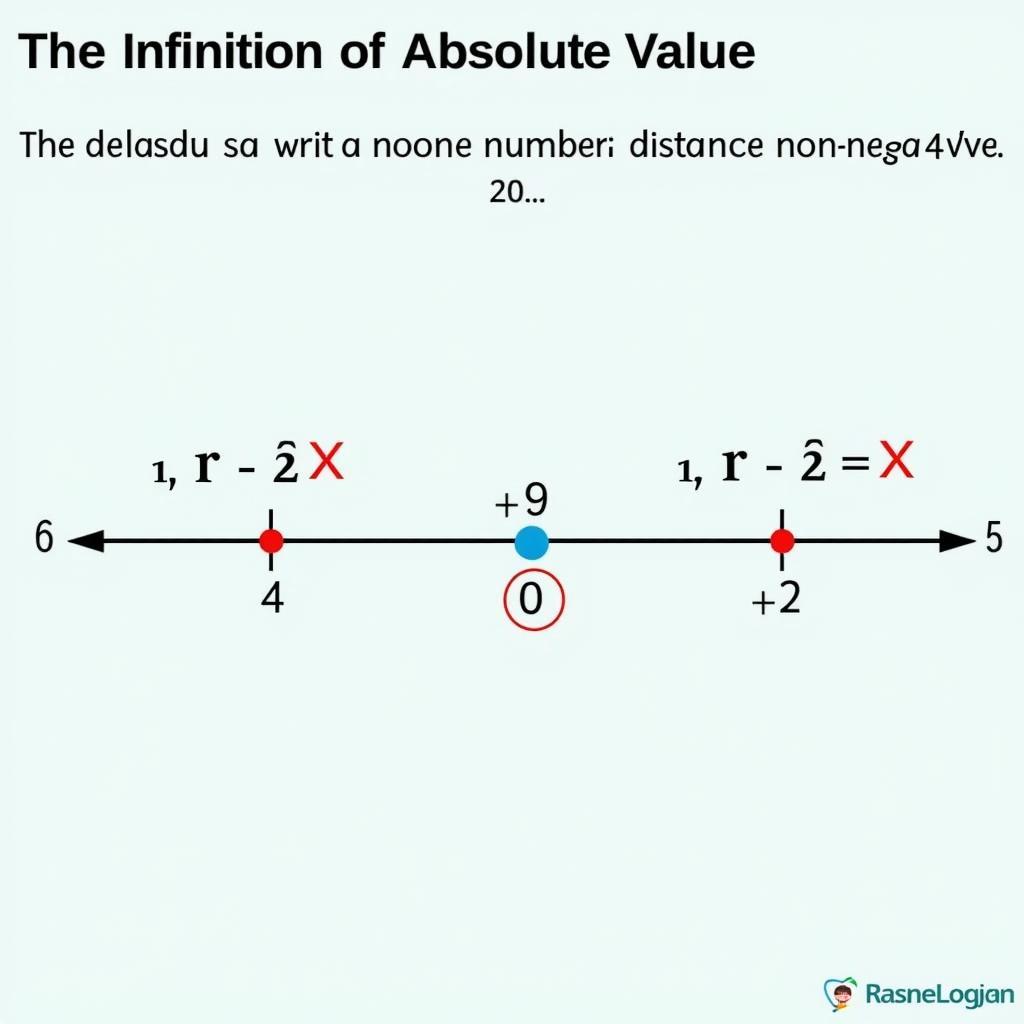 Định nghĩa trị tuyệt đối trên trục số
Định nghĩa trị tuyệt đối trên trục số
Các Tính Chất Quan Trọng Của Trị Tuyệt Đối Lớp 10
Có một số tính chất quan trọng của trị tuyệt đối mà bạn cần ghi nhớ:
- |x| ≥ 0 với mọi x thuộc R.
- |x| = 0 khi và chỉ khi x = 0.
- |x.y| = |x|.|y|
- |x/y| = |x|/|y| (với y ≠ 0)
- |-x| = |x|
Nắm vững các tính chất này sẽ giúp bạn biến đổi và giải quyết các bài toán liên quan đến công thức trị tuyệt đối lớp 10 một cách linh hoạt.
Phương Trình và Bất Phương Trình Chứa Trị Tuyệt Đối
Một phần quan trọng khi học về công thức trị tuyệt đối lớp 10 là giải phương trình và bất phương trình chứa trị tuyệt đối. Dưới đây là một số dạng cơ bản:
- |x| = a (a ≥ 0) <=> x = a hoặc x = -a
- |x| < a (a > 0) <=> -a < x < a
- |x| > a (a > 0) <=> x > a hoặc x < -a
Việc thành thạo các dạng này sẽ giúp bạn giải quyết nhiều bài toán phức tạp hơn. Bạn có muốn tìm hiểu thêm về bài tập về công thức cộng vận tốc?
Ứng Dụng Của Công Thức Trị Tuyệt Đối Trong Thực Tế
Công thức trị tuyệt đối không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tiễn. Ví dụ, trong vật lý, trị tuyệt đối được sử dụng để tính quãng đường, độ dịch chuyển. Trong đời sống, trị tuyệt đối có thể được sử dụng để tính toán sai số, độ lệch. Việc hiểu rõ diện tích hình thang cân công thức cũng rất hữu ích trong nhiều tình huống thực tế.
Trả Lời Các Câu Hỏi
What “công thức trị tuyệt đối lớp 10”?
Công thức trị tuyệt đối lớp 10 bao gồm định nghĩa, tính chất và cách giải phương trình, bất phương trình chứa trị tuyệt đối.
Who “công thức trị tuyệt đối lớp 10”?
Học sinh lớp 10 sẽ học về công thức trị tuyệt đối.
When “công thức trị tuyệt đối lớp 10”?
Công thức trị tuyệt đối thường được học trong học kỳ 1 của lớp 10.
Where “công thức trị tuyệt đối lớp 10”?
Công thức trị tuyệt đối được học trong chương trình toán lớp 10 tại trường học.
Why “công thức trị tuyệt đối lớp 10”?
Công thức trị tuyệt đối quan trọng vì nó là nền tảng cho nhiều kiến thức toán học nâng cao.
How “công thức trị tuyệt đối lớp 10”?
Học sinh có thể học công thức trị tuyệt đối qua sách giáo khoa, bài giảng của giáo viên và các nguồn tài liệu trực tuyến. Tìm hiểu thêm về công thức tính đường kính tương đương có thể mở rộng kiến thức của bạn.
 Ứng dụng của trị tuyệt đối
Ứng dụng của trị tuyệt đối
Kết Luận
Công thức trị tuyệt đối lớp 10 là một kiến thức quan trọng và có tính ứng dụng cao. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và đầy đủ về chủ đề này. Hãy luyện tập thường xuyên để nắm vững kiến thức và vận dụng thành thạo công thức trị tuyệt đối vào giải quyết các bài toán. Bạn cũng có thể tìm hiểu thêm về bài tập công thức hóa học lớp 8 để củng cố kiến thức hóa học của mình.
FAQ
-
Nêu định nghĩa trị tuyệt đối? Trị tuyệt đối của một số là khoảng cách từ số đó đến 0 trên trục số.
-
Tính chất cơ bản của trị tuyệt đối là gì? Trị tuyệt đối của một số luôn không âm, bằng 0 khi và chỉ khi số đó bằng 0.
-
Làm thế nào để giải phương trình |x| = a? Nếu a ≥ 0, phương trình có nghiệm x = a hoặc x = -a. Nếu a < 0, phương trình vô nghiệm.
-
Bất phương trình |x| < a được giải như thế nào? Nếu a > 0, bất phương trình có nghiệm -a < x < a. Nếu a ≤ 0, bất phương trình vô nghiệm.
-
Ứng dụng của trị tuyệt đối trong thực tế là gì? Trị tuyệt đối được ứng dụng trong vật lý để tính quãng đường, độ dịch chuyển, và trong nhiều lĩnh vực khác để tính toán sai số, độ lệch. Công thức tính nhiệt lượng cung cấp cho khối khí cũng là một ví dụ về ứng dụng của các công thức toán học trong vật lý.
-
Tại sao trị tuyệt đối của một số luôn không âm? Vì trị tuyệt đối biểu diễn khoảng cách, mà khoảng cách luôn là một giá trị không âm.
-
Làm thế nào để tính trị tuyệt đối của một số âm? Lấy số đối của số âm đó.
-
Trị tuyệt đối của 0 là bao nhiêu? 0.
-
Khi nào thì |x| = -x? Khi x ≤ 0.
-
Khi nào thì |x| = x? Khi x ≥ 0.
